Wie Rechnet Man Die Höhe Eines Dreiecks Aus

Okay, Leute, mal ehrlich: Wer von uns hat in Mathe nicht mal komplett auf Durchzug geschaltet? Ich bekenne mich schuldig! Und Dreiecke, speziell die Höhe davon zu berechnen, war für mich immer so ein bisschen wie der Versuch, mit Stäbchen Spaghetti zu essen – frustrierend und am Ende kleckert man trotzdem alles voll. Aber keine Panik! Wir kriegen das hin. Versprochen. Kaffee ist parat? Gut, dann legen wir los!

Die Höhe? Was'n das überhaupt?

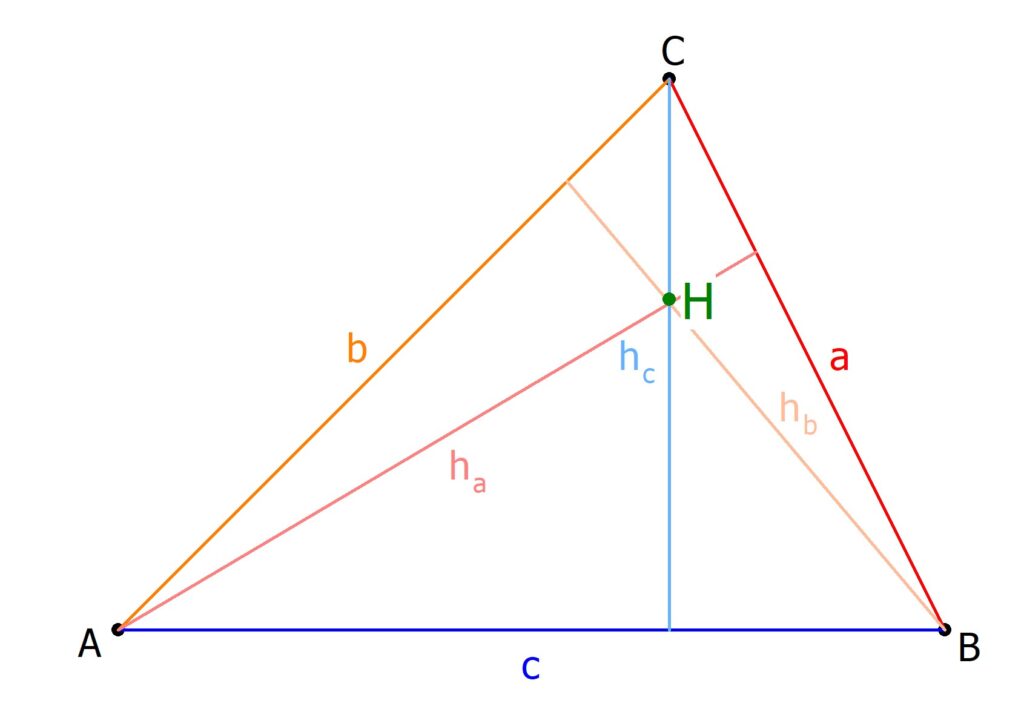
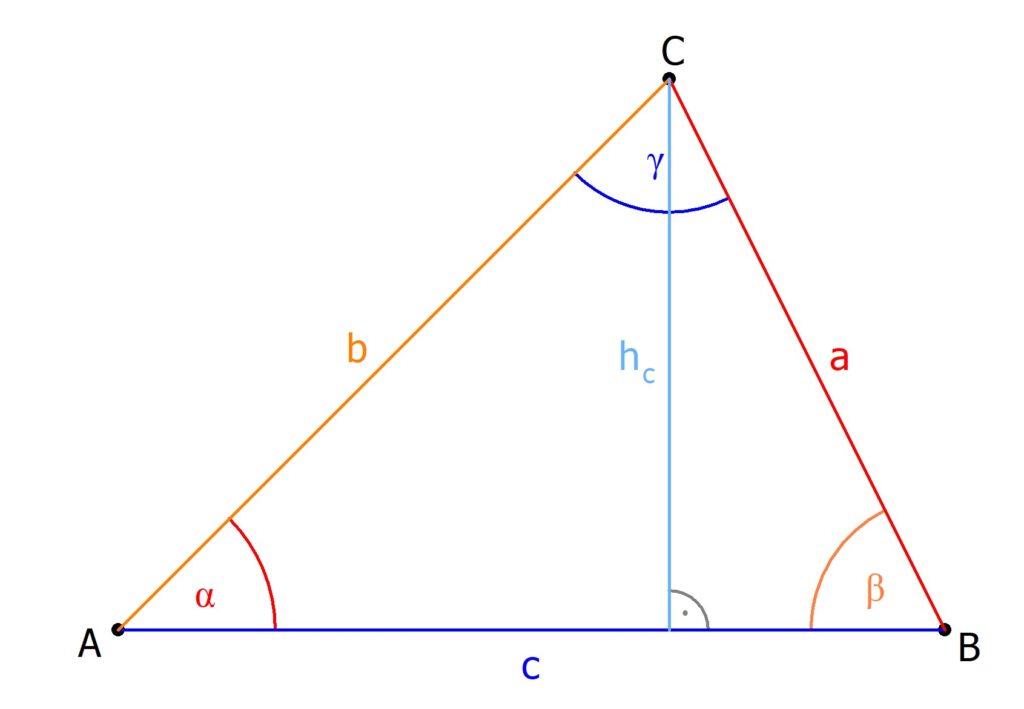
Stell dir vor, ein Dreieck ist ein Zelt. Die Höhe ist dann quasi der höchste Punkt des Zeltes, gemessen vom Boden (also der Grundseite) bis zur Spitze. Und das Wichtigste: Sie steht immer senkrecht auf der Grundseite. Also im 90-Grad-Winkel. Stell dir vor, sie ist ein supersauberer, perfekt gerader Laserstrahl, der vom Boden bis zur Spitze zielt. Wenn der Laser schief wäre, würde das Zelt zusammenbrechen! Und das wollen wir ja nicht.

Warum ist das wichtig? Naja, wenn du die Fläche eines Dreiecks berechnen willst (und wer will das nicht irgendwann mal? Vielleicht, um auszurechnen, wie viel Stoff du für ein Dreieckskostüm brauchst?), dann brauchst du die Höhe. Ohne Höhe keine Party, äh, Fläche!

Die Formel, die dich zum Mathe-Guru macht (fast)

Okay, jetzt kommt der Teil, vor dem sich viele fürchten: die Formel. Aber keine Sorge, ich hab' sie gezähmt. Sie ist eigentlich ganz lieb. Sie lautet:

Fläche = (Grundseite * Höhe) / 2

Oder, wenn wir die Höhe suchen, drehen wir das Ganze einfach um:

Höhe = (2 * Fläche) / Grundseite

Ja, das ist alles! Kein Hexenwerk, oder? Stell dir vor, du bist ein Mathe-Ninja und jonglierst mit diesen Formeln. "Hoi!" - die Fläche! "Hoi!" - die Grundseite! "Hoi!" - die Höhe! Okay, vielleicht nicht ganz Ninja, eher so ein... freundlicher Mathe-Teddybär.

Verschiedene Dreiecke, verschiedene Höhen (Drama!)

Es gibt ja nicht nur *das eine* Dreieck. Nein, nein, nein! Es gibt:

Gleichseitige Dreiecke: Alle Seiten sind gleich lang, alle Winkel sind gleich groß. Hier ist die Höhe am einfachsten zu berechnen, weil sie das Dreieck perfekt in zwei identische Hälften teilt.
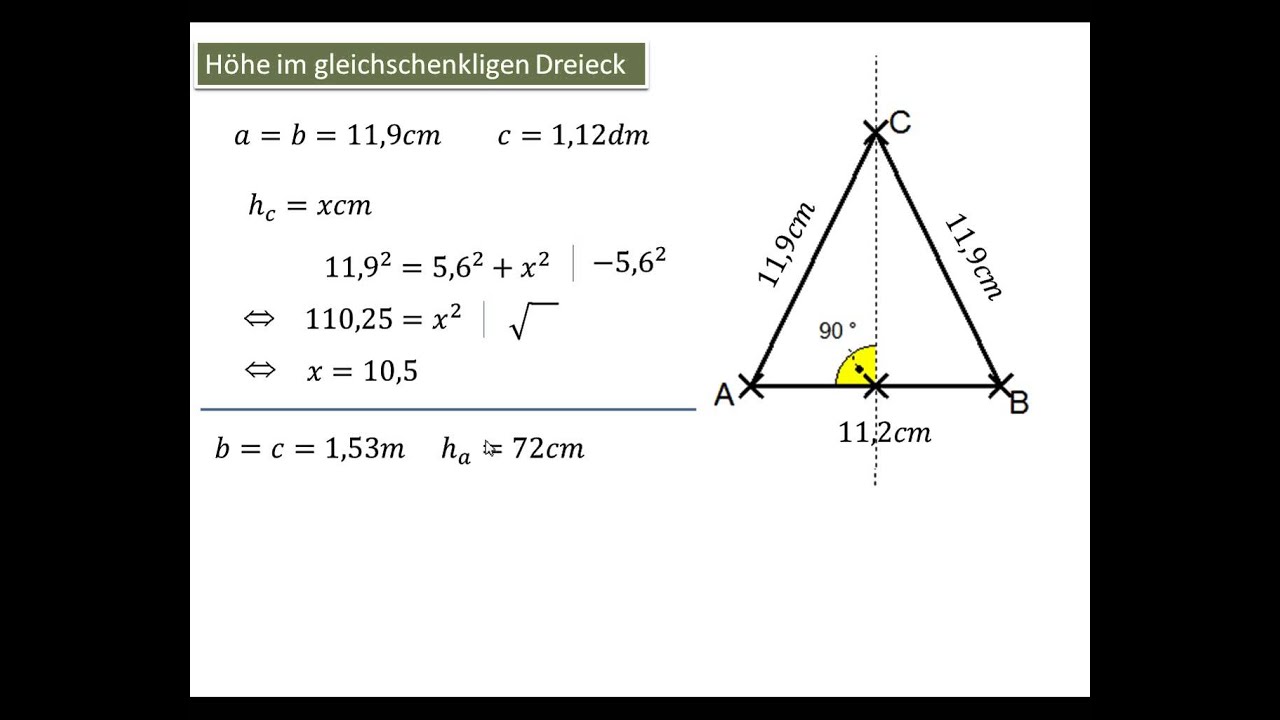
Gleichschenklige Dreiecke: Zwei Seiten sind gleich lang. Hier musst du aufpassen, welche Seite die Grundseite ist, denn davon hängt ab, wo die Höhe hinführt.
Rechtwinklige Dreiecke: Einer der Winkel ist 90 Grad. Hier ist es super einfach, weil eine der Seiten bereits die Höhe ist! Jackpot!
Spitzwinklige Dreiecke: Alle Winkel sind kleiner als 90 Grad. Hier ist die Höhe innerhalb des Dreiecks. Alles easy!
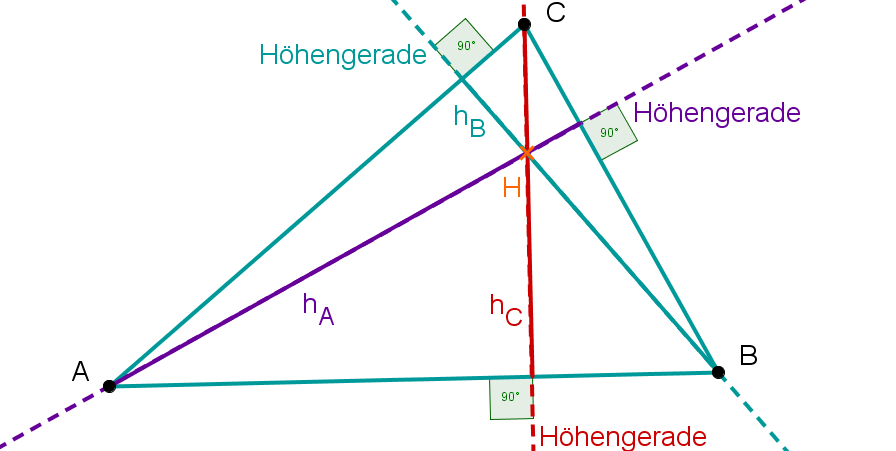
Stumpfwinklige Dreiecke: Ein Winkel ist größer als 90 Grad. Hier wird's knifflig! Die Höhe liegt *außerhalb* des Dreiecks. Ja, richtig gelesen! Stell dir vor, du musst das Dreieck verlängern, um die Höhe zu finden. Verrückt, aber wahr!

Das ist wie bei einer Reality-Show: Jedes Dreieck hat seine eigenen Dramen und Eigenheiten.

Beispiel gefällig? (Na klar!)

Nehmen wir an, wir haben ein Dreieck mit einer Fläche von 20 Quadratzentimetern und einer Grundseite von 5 Zentimetern. Was ist die Höhe?

Also, unsere Formel lautet: Höhe = (2 * Fläche) / Grundseite

Wir setzen ein: Höhe = (2 * 20) / 5

Das ergibt: Höhe = 40 / 5 = 8 Zentimeter

Tadaaa! Die Höhe beträgt 8 Zentimeter. Du hast es geschafft! Du bist jetzt offiziell ein Dreieckshöhen-Berechnungs-Meister! (Okay, vielleicht nicht *ganz* Meister, aber zumindest ein... engagierter Lehrling.)

Tricks und Tipps vom Profi (also, von mir...)

Zeichne! Ein Bild sagt mehr als tausend Formeln. Skizziere das Dreieck, zeichne die Höhe ein und markiere die gegebenen Werte. Das hilft ungemein!
Achte auf die Einheiten! Wenn die Fläche in Quadratzentimetern angegeben ist, muss die Grundseite auch in Zentimetern sein. Sonst gibt's Kuddelmuddel!
Wenn du nicht weiterweißt: Frag jemanden! Es gibt keine Schande darin, um Hilfe zu bitten. Oder schau dir ein Erklärvideo an. YouTube ist dein Freund!
Hab Spaß! Mathe muss nicht langweilig sein. Stell dir vor, du bist ein Detektiv, der ein kniffliges Rätsel löst.

Und das Wichtigste: Gib nicht auf! Auch wenn du am Anfang Schwierigkeiten hast, bleib dran. Übung macht den Meister (oder zumindest den passablen Dreieckshöhen-Berechner). Und denk dran: Selbst Einstein hatte mal einen schlechten Tag in Mathe! (Okay, das ist vielleicht eine Übertreibung, aber es klingt gut, oder?)

So, jetzt geh raus und berechne Dreieckshöhen! Die Welt braucht mehr Menschen, die Dreiecke verstehen. Und wenn du mal wieder Spaghetti mit Stäbchen essen willst, viel Glück! (Ich bleibe lieber bei der Gabel.)