Wie Viele Nullstellen Hat Eine Funktion 3 Grades

Wer hat nicht schon einmal in den Sternenhimmel geblickt und sich gefragt: Wie funktioniert das alles? Mathematik, oft als trocken und kompliziert abgetan, ist in Wahrheit ein faszinierendes Werkzeug, um die Welt um uns herum zu verstehen. Und mitten in diesem Universum der Zahlen tummeln sich die Funktionen – kleine Helfer, die Beziehungen beschreiben und Vorhersagen ermöglichen. Eine besonders interessante Spezies sind die Funktionen 3. Grades, auch kubische Funktionen genannt. Aber was macht sie so spannend, und vor allem: Wie viele Nullstellen haben sie?
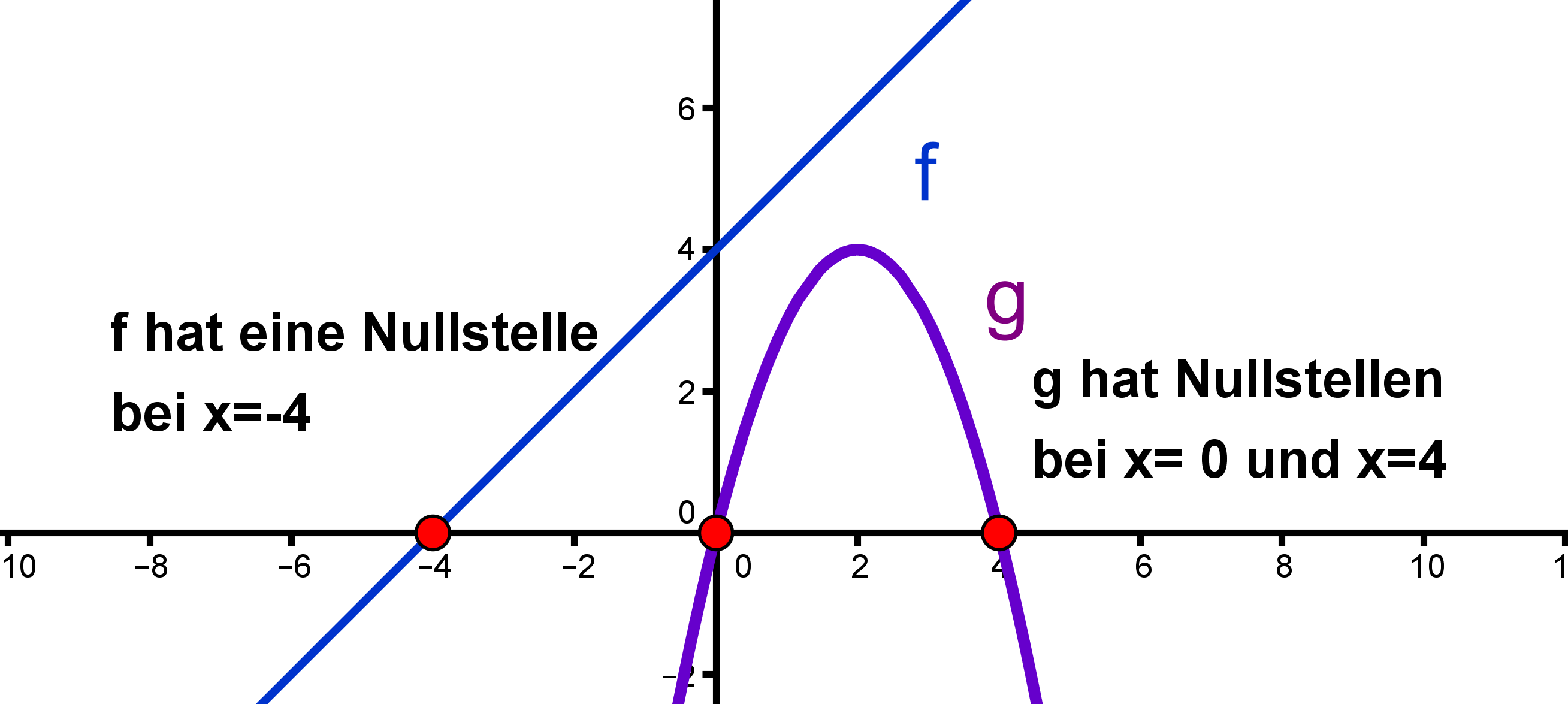
Die Frage nach den Nullstellen einer Funktion 3. Grades ist mehr als nur eine akademische Übung. Sie hilft uns, das Verhalten dieser Funktionen besser zu verstehen und ihre Anwendungen in der realen Welt zu erkennen. Nullstellen sind die Punkte, an denen der Graph der Funktion die x-Achse schneidet – die Werte von x, für die die Funktion den Wert Null annimmt. In der Praxis bedeutet das, dass wir mit ihrer Hilfe kritische Punkte identifizieren können, wo sich ein System in einem bestimmten Zustand befindet. Stellen Sie sich beispielsweise vor, Sie modellieren das Wachstum einer Population mit einer kubischen Funktion. Die Nullstellen könnten dann den Zeitpunkt darstellen, an dem die Population ausstirbt oder einen kritischen Schwellenwert erreicht.
Die Anwendung von Funktionen 3. Grades ist vielfältig. In der Physik werden sie zur Beschreibung von Bewegungsvorgängen verwendet, in der Wirtschaft zur Modellierung von Kostenfunktionen und in der Informatik zur Optimierung von Algorithmen. Denken Sie an eine Achterbahn: Die Kurven und Drehungen lassen sich oft mit kubischen Funktionen beschreiben. Auch bei der Gestaltung von Oberflächen in der Computergraphik spielen sie eine wichtige Rolle.
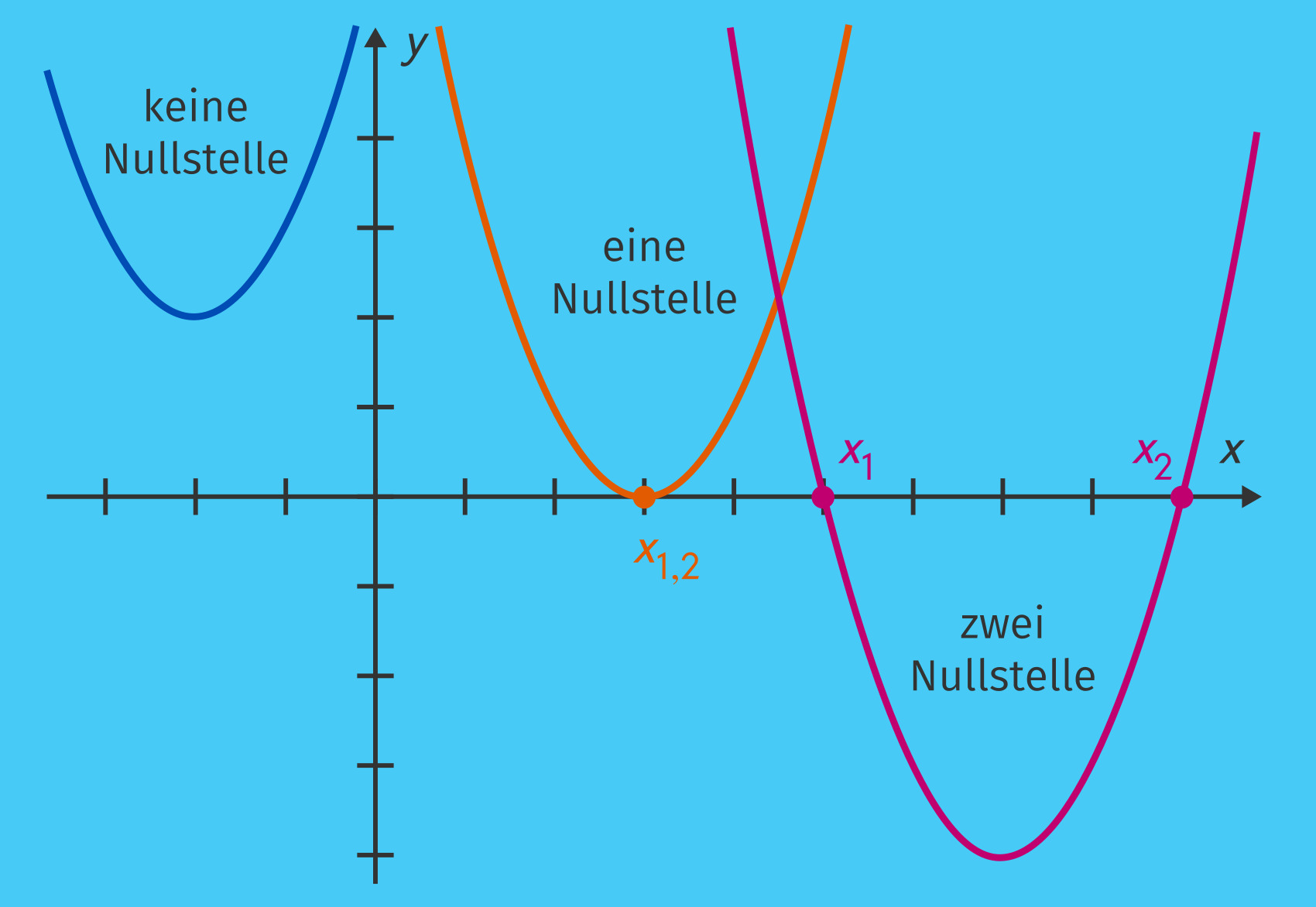
Aber zurück zur Kernfrage: Wie viele Nullstellen hat eine Funktion 3. Grades? Die Antwort ist: es können eine, zwei oder drei sein. Das hängt von der Form der Funktion ab. Eine Funktion 3. Grades hat immer mindestens eine reelle Nullstelle, da ihr Graph entweder von "unten links" nach "oben rechts" oder von "oben links" nach "unten rechts" verläuft und somit zwangsläufig die x-Achse schneiden muss. Wenn die Funktion mehr als eine Nullstelle hat, können diese entweder alle reell und unterschiedlich sein, oder es gibt eine reelle Nullstelle und ein Paar konjugiert komplexe Nullstellen, die sich nicht auf der x-Achse darstellen lassen. Es ist auch möglich, dass eine Nullstelle mehrfach vorkommt – man spricht dann von einer doppelten oder dreifachen Nullstelle.
Um das Thema noch besser zu verstehen und Spaß daran zu haben, hier ein paar praktische Tipps: Visualisieren Sie die Funktionen! Nutzen Sie Online-Graphzeichner oder Programme wie GeoGebra, um Funktionen 3. Grades zu zeichnen und experimentieren Sie mit verschiedenen Parametern. Beobachten Sie, wie sich die Anzahl und Lage der Nullstellen verändern. Üben Sie das Lösen von Gleichungen 3. Grades! Es gibt zwar keine allgemeingültige Formel wie bei quadratischen Gleichungen, aber verschiedene numerische Verfahren können helfen, die Nullstellen näherungsweise zu bestimmen. Und schließlich: Suchen Sie nach Anwendungen in Ihrer Umgebung! Wenn Sie ein bestimmtes Phänomen besser verstehen wollen, versuchen Sie, es mit einer Funktion 3. Grades zu modellieren. So wird Mathematik lebendig und relevant.
Also, keine Angst vor kubischen Funktionen! Sie sind faszinierende Werkzeuge, um die Welt zu verstehen, und die Suche nach ihren Nullstellen ist ein spannendes Abenteuer.