Wie Zeichnet Man Einen Inkreis Im Dreieck
Na, schon wieder über Mathe gebeugt? Keine Panik, ich hab' da was für dich. Heute reden wir über den Inkreis im Dreieck. Ja, genau, dieser Kreis, der so perfekt in das Dreieck eingepasst ist, als hätte er nie etwas anderes vorgehabt. Klingt kompliziert? Überhaupt nicht! Versprochen!
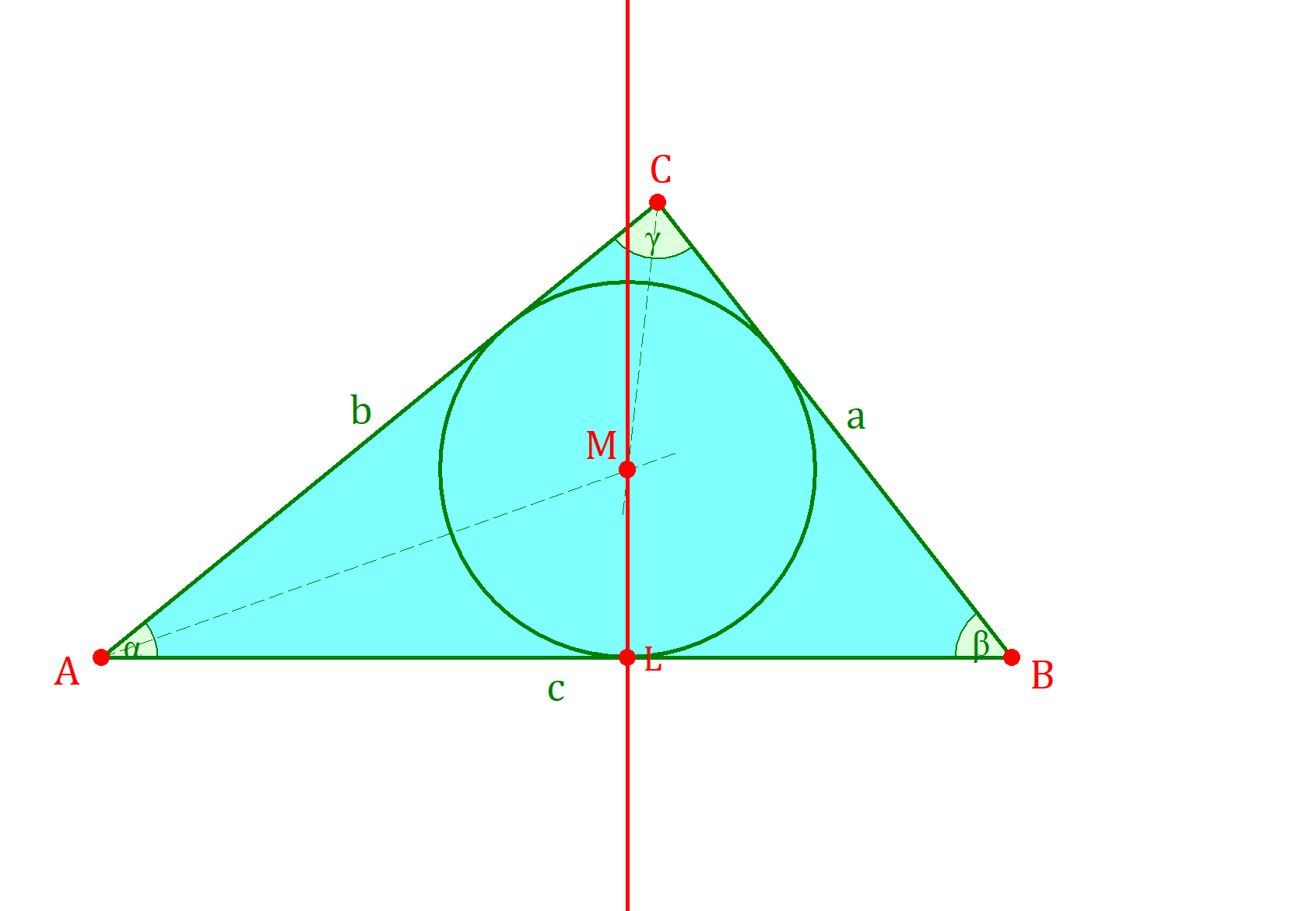
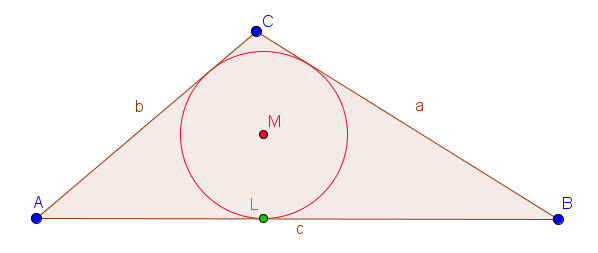
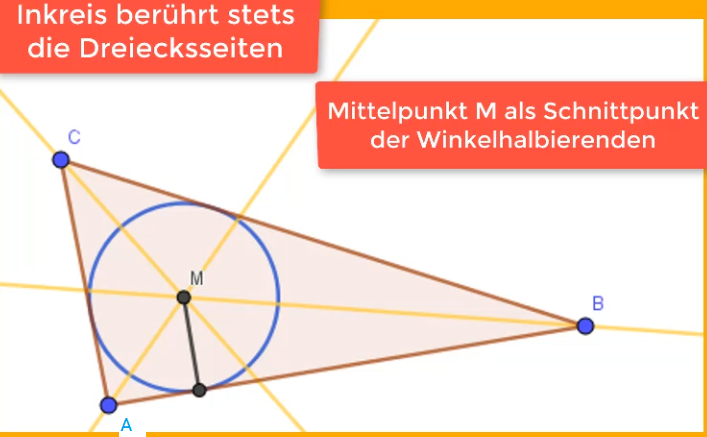
Also, was ist eigentlich ein Inkreis? Stell dir vor, du hast ein Dreieck, egal welches. Ein spitzes, ein stumpfes, ein gleichseitiges… ganz egal! Und dann malst du einen Kreis rein, der alle drei Seiten von innen berührt. Wie eine kleine Kugel, die es sich in einer dreieckigen Schale gemütlich macht. Das ist der Inkreis. Und der Mittelpunkt dieses Kreises? Der nennt sich Inkreismittelpunkt. Überraschung!
Aber wie zeichnet man das Ding nun? Keine Sorge, wir brauchen keinen Zauberstab oder einen besonders schlau aussehenden Zirkel. Nur einen ganz normalen Zirkel, ein Lineal und ein bisschen Geduld (und vielleicht einen Kaffee, um die Nerven zu beruhigen – Mathe kann manchmal ganz schön aufregend sein, oder?).
Schritt 1: Winkelhalbierende, die heimlichen Stars
Das Geheimnis des Inkreises liegt in den Winkelhalbierenden. Was sind das? Stell dir vor, du halbierst jeden Winkel des Dreiecks genau in der Mitte. Also, teilst ihn in zwei gleiche Teile. Jede dieser Linien, die den Winkel teilt, ist eine Winkelhalbierende. Klingt langweilig? Ist aber super wichtig!
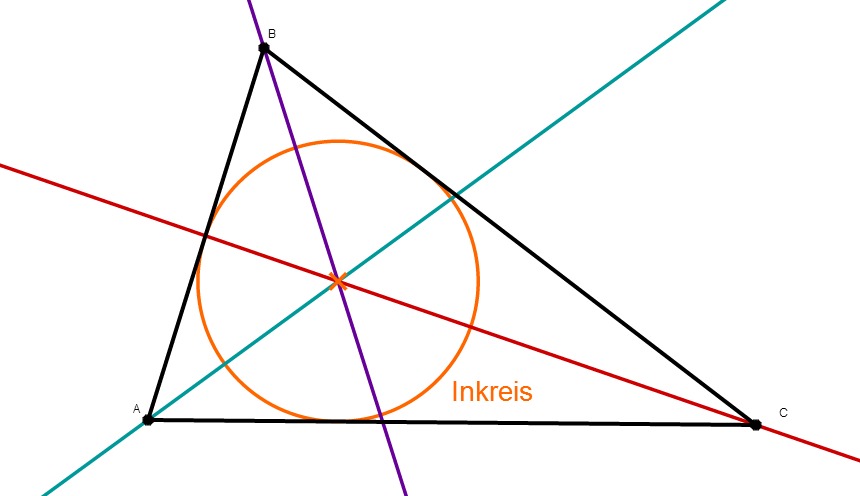
Wie zeichnet man die? Am einfachsten mit dem Zirkel! Steche mit dem Zirkel in den Eckpunkt des Winkels ein und zeichne einen kleinen Bogen, der beide Schenkel des Winkels schneidet. Dann steche in die Schnittpunkte ein und zeichne von dort zwei weitere Bögen, die sich irgendwo im Inneren des Winkels treffen. Und der Schnittpunkt dieser Bögen? Der liegt genau auf der Winkelhalbierenden! Verbinde den Eckpunkt mit diesem Schnittpunkt und tadaaa, du hast deine Winkelhalbierende! Macht Spaß, oder?
Schritt 2: Der Inkreismittelpunkt, das magische Zentrum
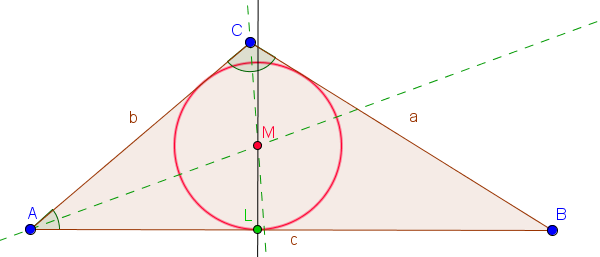
Jetzt kommt der Clou! Du musst nämlich nicht alle drei Winkelhalbierenden zeichnen. Es reichen zwei. Denn: Der Schnittpunkt von zwei Winkelhalbierenden ist nämlich genau der Inkreismittelpunkt. Wie cool ist das denn bitte?
Warum das so ist? Tja, das ist ein bisschen komplizierter und hat was mit Geometrie und Abständen zu tun. Aber vertrau mir einfach, es funktioniert. Wenn du ganz genau sein willst, kannst du natürlich auch die dritte Winkelhalbierende zeichnen. Sie sollte auch durch denselben Punkt gehen. Wenn nicht, hast du dich vielleicht irgendwo vermessen. Aber keine Panik, das passiert den Besten!
Schritt 3: Der Radius und das große Finale
Jetzt haben wir den Mittelpunkt! Aber woher wissen wir, wie groß der Kreis sein muss? Kein Problem! Wir brauchen den Radius.
Der Radius ist der Abstand vom Inkreismittelpunkt zu einer der Seiten des Dreiecks. Aber Achtung! Du musst den kürzesten Abstand nehmen, also senkrecht zur Seite. Das heißt, du musst vom Inkreismittelpunkt ein Lot auf eine der Seiten fällen. Am besten nimmst du dafür ein Geodreieck (oder versuchst es Augenmaß, wenn du mutig bist!).
Diesen senkrechten Abstand misst du dann mit deinem Lineal. Das ist der Radius deines Inkreises! Jetzt steckst du den Zirkel in den Inkreismittelpunkt, stellst den Radius ein und ziehst den Kreis. Fertig! Dein Inkreis ist geboren!
Extra-Tipp: Übung macht den Meister!
Je öfter du das machst, desto besser wird es. Und keine Sorge, wenn es beim ersten Mal nicht perfekt klappt. Mathe ist wie Fahrradfahren: Am Anfang fällt man hin, aber irgendwann klappt's wie von selbst. Und hey, wenn gar nichts geht, frag einfach nochmal nach! Dafür sind Freunde ja da (und das Internet sowieso)! Viel Spaß beim Zeichnen!