Woher Weiß Man Ob Ein Dreieck Rechtwinklig Ist

Hallo, liebe Freunde der Geometrie! Habt ihr euch jemals gefragt, wie man eigentlich herausfindet, ob ein Dreieck einen perfekten rechten Winkel hat? Keine Sorge, ihr braucht keinen Winkelmesser im Gepäck, denn es gibt ein paar richtig coole Tricks, die das Leben (und Mathe!) viel einfacher machen. Und hey, wer weiß, vielleicht beeindruckt ihr ja beim nächsten Picknick eure Freunde mit eurem Dreiecks-Wissen!

Also, lasst uns eintauchen in die faszinierende Welt der rechtwinkligen Dreiecke!

Der Satz des Pythagoras: Dein bester Freund!

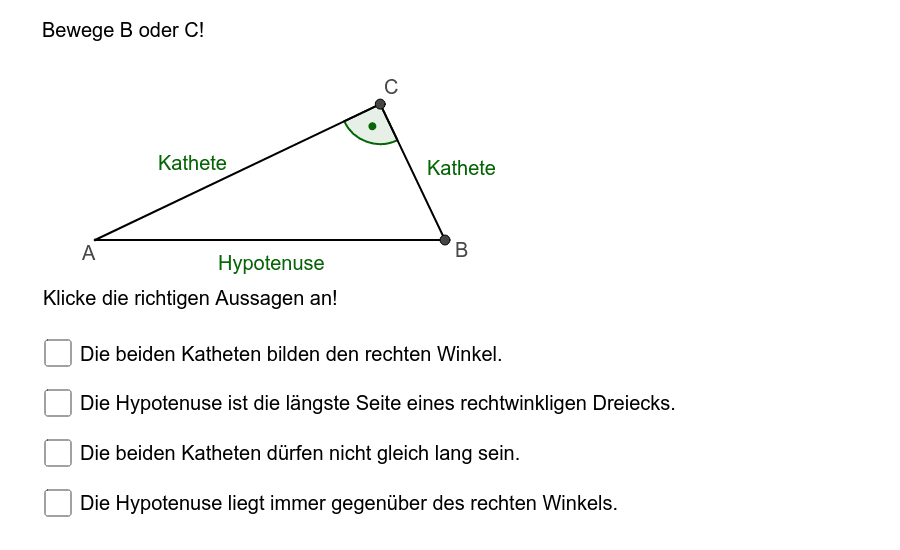
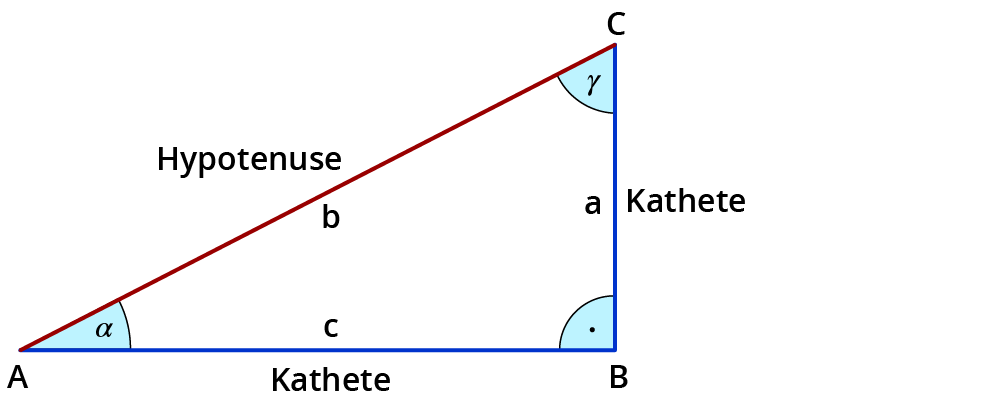
Okay, Hand aufs Herz: Der Name klingt vielleicht erstmal ein bisschen einschüchternd, aber der Satz des Pythagoras ist wirklich kein Monster. Im Gegenteil, er ist super hilfreich! Er besagt nämlich, dass in einem rechtwinkligen Dreieck das Quadrat der längsten Seite (der Hypotenuse) gleich der Summe der Quadrate der beiden kürzeren Seiten (den Katheten) ist. Puh, langer Satz! Aber keine Panik, wir brechen das mal runter.

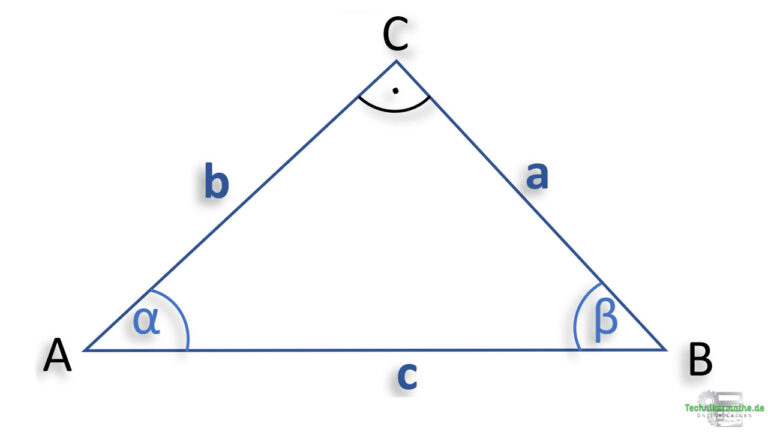
Denkt an diese Formel: a² + b² = c²

Dabei sind:

a und b die Längen der beiden kürzeren Seiten (Katheten)
c die Länge der längsten Seite (Hypotenuse)

Moment mal, Quadrate? Katheten? Hypotenuse? Keine Sorge, wir machen ein Beispiel:

Stell dir vor, du hast ein Dreieck mit Seitenlängen von 3, 4 und 5 cm. Ist das ein rechtwinkliges Dreieck? Lass uns den Pythagoras fragen!

a = 3, b = 4, c = 5

Also: 3² + 4² = 9 + 16 = 25

Und: 5² = 25

Tadaaa! 3² + 4² = 5² stimmt! Das bedeutet, unser Dreieck mit den Seiten 3, 4 und 5 ist tatsächlich ein rechtwinkliges Dreieck! Applaus für Pythagoras (und für dich)!

Die Umkehrung des Satzes: Ein Detektivtrick!

Der Clou ist: Der Satz des Pythagoras funktioniert auch umgekehrt! Wenn du also die Seitenlängen eines Dreiecks kennst und feststellst, dass a² + b² = c² gilt, dann weißt du automatisch, dass das Dreieck einen rechten Winkel hat. Das ist wie ein Detektivtrick für Geometrie-Fans!

Du musst also nicht unbedingt einen Winkelmesser zücken. Einfach die Seitenlängen quadrieren und schauen, ob die Rechnung aufgeht. Genial, oder?

Warum ist das überhaupt wichtig?

Gute Frage! Rechtwinklige Dreiecke sind überall in unserem Leben. Sie stecken in der Architektur von Gebäuden, in der Konstruktion von Brücken und sogar in der Navigation! Wenn du verstehst, wie rechtwinklige Dreiecke funktionieren, kannst du plötzlich die Welt um dich herum mit ganz anderen Augen sehen. Du wirst zum Geometrie-Ninja!

Stell dir vor, du baust ein Vogelhaus und willst sicherstellen, dass das Dach den richtigen Winkel hat. Oder du planst einen Garten und möchtest ein perfektes rechteckiges Beet anlegen. Mit dem Satz des Pythagoras bist du bestens gerüstet!

Andere Winkel als Beweis nutzen

Nun gut, wenn du jetzt keinen Bock auf den Satz des Pythagoras hast (obwohl er echt super ist!), gibt es noch eine andere Möglichkeit, ein rechtwinkliges Dreieck zu erkennen. Erinnere dich: Die Summe der Innenwinkel in einem Dreieck beträgt immer 180 Grad. Wenn du also weißt, dass einer der Winkel 90 Grad ist, dann ist es ein rechtwinkliges Dreieck. Klar, dazu brauchst du dann doch einen Winkelmesser... Aber hey, Optionen sind gut!

Achte darauf: Du brauchst nur einen Winkel zu messen. Wenn der 90 Grad hat, ist die Sache klar!

Also, was haben wir gelernt?

Wir haben gelernt, dass wir rechtwinklige Dreiecke mit dem Satz des Pythagoras und seiner Umkehrung erkennen können. Und wir haben gelernt, dass Geometrie gar nicht so staubtrocken ist, wie man vielleicht denkt! Sie kann sogar richtig Spaß machen und uns helfen, die Welt um uns herum besser zu verstehen.

Und jetzt? Jetzt bist du dran! Nimm dir ein paar Stifte, ein Papier und vielleicht sogar ein Lineal und probier es selbst aus. Entdecke die faszinierende Welt der rechtwinkligen Dreiecke und lass dich von der Schönheit der Geometrie inspirieren. Wer weiß, vielleicht entdeckst du ja dein inneres Mathe-Genie! Und denk daran: Mathe ist nicht nur Rechnen, sondern auch ein Abenteuer!

Also, los geht's! Die Welt der rechtwinkligen Dreiecke wartet auf dich!