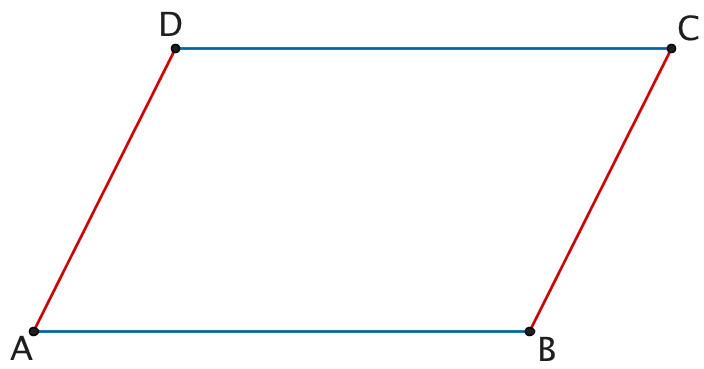
Zeigen Sie Dass Abcd Ein Parallelogramm Ist
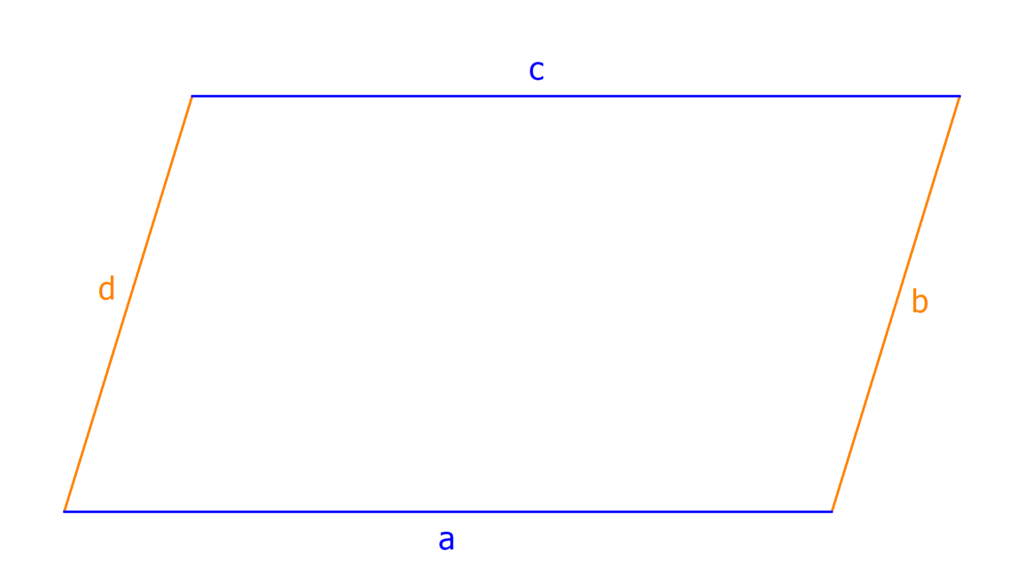
Na, schon wieder Geometrie-Hausaufgaben am Start? Lass uns mal über Parallelogramme quatschen. Genauer gesagt: Wie zeigen wir, dass ABCD tatsächlich ein Parallelogramm ist? Keine Panik, ist einfacher als 'ne Wurzel ziehen (oder war's doch andersrum?).
Okay, angenommen, du hast so ein Viereck ABCD vor dir liegen. Sieht vielleicht verdächtig nach Parallelogramm aus, aber "sieht aus" reicht ja bekanntlich nicht, oder? Wir brauchen Beweise! Keine halben Sachen, wir sind schließlich Mathematiker (oder so ähnlich).
Methode 1: Gegenüberliegende Seiten parallel
Der Klassiker! Ein Parallelogramm ist ja definiert als Viereck, bei dem die gegenüberliegenden Seiten parallel sind. Klingt logisch, oder? Aber wie zeigst du das konkret?
Du könntest zum Beispiel die Steigungen der Linien AB und CD berechnen. Sind die Steigungen gleich? Super! Dann sind die Linien schon mal parallel. Das gleiche Spielchen machst du dann noch mit den Linien AD und BC. Und voila! Wenn beide Paare gegenüberliegender Seiten parallel sind, hast du den Beweis! Quasi checkmate für ABCD als Parallelogramm.
Aber was, wenn du keine Steigungen berechnen willst? Keine Sorge, es gibt noch andere Wege! Wir sind ja nicht auf eine einzige Methode festgelegt. Wäre ja langweilig, oder?
Methode 2: Gegenüberliegende Seiten gleich lang
Ein weiteres Kriterium: Wenn die gegenüberliegenden Seiten gleich lang sind, dann ist ABCD ebenfalls ein Parallelogramm! Klingt fast zu einfach, oder? Aber es funktioniert wirklich. (Vertrau mir, ich bin fast ein Mathematiker.)
Wie misst du die Länge der Seiten? Mit dem guten alten Satz des Pythagoras natürlich! Oder, falls du's eleganter magst, mit der Abstandsformel. Ist ja im Prinzip dasselbe, nur anders verpackt. Du berechnest also die Länge von AB und CD. Stimmen die überein? Perfekt! Dann AD und BC. Auch gleich lang? Jackpot! ABCD ist offiziell ein Parallelogramm. Jubel! 🎉
Methode 3: Gegenüberliegende Winkel gleich groß
Wir werden kreativ! Diesmal schauen wir uns die Winkel an. Wenn die gegenüberliegenden Winkel gleich groß sind, dann… du ahnst es schon… ist ABCD ein Parallelogramm!
Winkel messen? Je nachdem, wie deine Aufgabe aussieht, könnte das mit Geodreieck klappen, oder du berechnest die Winkel über Vektoren (wird dann etwas komplizierter, aber hey, wer sagt, dass Mathe immer einfach sein muss?). Wenn also Winkel A = Winkel C und Winkel B = Winkel D, dann ist alles in Butter. Parallelogramm confirmed!
Aber Achtung! Nur *ein* Paar gleicher Winkel reicht nicht! Denk dran, ein Rechteck hat auch zwei Paare gleicher Winkel, ist aber nicht zwingend ein Parallelogramm, es sei denn, die Seiten sind nicht alle gleich lang (dann wäre es ein Quadrat! Geometrie ist manchmal echt verwirrend, oder?).
Methode 4: Diagonalen halbieren sich
Jetzt wird's tricky! Zeichne die Diagonalen AC und BD in dein Viereck ein. Schneiden die sich in der Mitte? Mit anderen Worten: Halbiert der Schnittpunkt beide Diagonalen? Wenn ja, bingo! Parallelogramm!
Wie findest du den Mittelpunkt einer Strecke? Na, mit der Mittelpunktsformel! (X1 + X2) / 2 und (Y1 + Y2) / 2. Ist der Mittelpunkt von AC derselbe wie der Mittelpunkt von BD? Dann haben wir unseren Beweis! Mission accomplished!
Methode 5: Ein Paar gegenüberliegender Seiten parallel und gleich lang
Die ultimative Methode für Faule (oder Effiziente, je nachdem, wie man's sieht). Wenn ein Paar gegenüberliegender Seiten sowohl parallel als auch gleich lang ist, dann ist ABCD ein Parallelogramm! Ein Beweis für die Effizienz in der Mathematik! 🎉
Du berechnest also die Steigung und die Länge von AB und CD. Sind sie gleich? Dann brauchst du AD und BC gar nicht mehr anzuschauen! Du hast gewonnen! 🥳
So, das waren die gängigsten Methoden, um zu zeigen, dass ABCD ein Parallelogramm ist. Wähle die Methode, die dir am einfachsten erscheint, schnapp dir deinen Stift und leg los! Und denk dran: Mathe kann auch Spaß machen! (Okay, manchmal vielleicht nicht. Aber meistens! 😉)