Zentrische Streckung Aufgaben Mit Lösungen Pdf

Hey du! Hast du jemals das Gefühl gehabt, dass Matheaufgaben aussehen wie Aliensprache? Keine Sorge, wir alle waren schon mal da. Besonders, wenn es um so etwas wie "Zentrische Streckung" geht. Klingt kompliziert, oder? Aber keine Panik! Wir tauchen heute ein in die Welt der zentrischen Streckung, bewaffnet mit Aufgaben, Lösungen und einer ganzen Menge Humor.

Stell dir vor, du stehst vor einem Spiegel. Dein Spiegelbild ist eine zentrische Streckung von dir selbst – nur eben anders platziert und vielleicht ein bisschen verzerrt, wenn der Spiegel ein komisches Format hat (oder du komische Grimassen ziehst!).

Was zum Teufel ist Zentrische Streckung überhaupt?

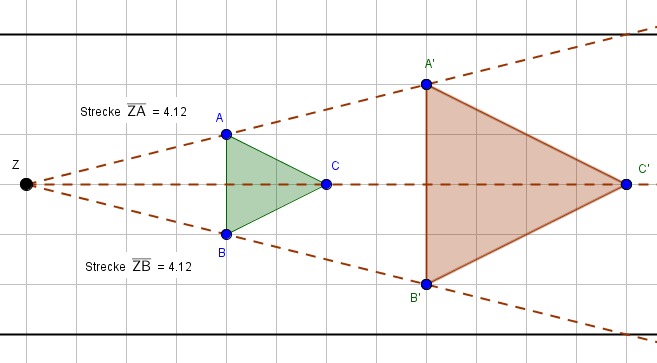
Ganz einfach: Die zentrische Streckung ist eine Art Vergrößerung oder Verkleinerung einer geometrischen Figur von einem bestimmten Punkt aus, dem Zentrum der Streckung. Denk an einen Beamer, der ein Bild auf eine Leinwand wirft. Das Bild auf der Leinwand ist eine zentrische Streckung des Bildes, das der Beamer erzeugt.

Der Clou: Alles wird proportional größer oder kleiner! Keine wilden Verzerrungen, die gar keinen Sinn ergeben. (Außer, du bist Salvador Dalí, dann sind Verzerrungen natürlich erlaubt.)

Und keine Sorge, falls du gerade denkst "Hä?". Wir schauen uns das gleich anhand von Aufgaben an, die du dir als PDF runterladen und lösen kannst!

Aufgaben, Aufgaben, überall Aufgaben!

Ja, ich weiß, das Wort "Aufgaben" kann manchmal Panik auslösen. Aber hey, betrachte es als ein Spiel! Eine Herausforderung, bei der du am Ende mit dem Wissen glänzen kannst, was eine zentrische Streckung ist. (Und vielleicht sogar deine Freunde damit beeindrucken... oder einfach nur verwirren. Beides ist okay.)

Wenn du nach zentrische Streckung Aufgaben mit Lösungen als PDF suchst, dann wirst du im Internet schnell fündig. Es gibt unzählige Ressourcen, die dir helfen können. Achte aber darauf, dass die Lösungen auch *wirklich* stimmen! Sonst lernst du am Ende etwas Falsches und stehst bei der nächsten Prüfung blöd da.

Pro-Tipp: Fang mit einfachen Aufgaben an! Es bringt nichts, sich gleich mit den kompliziertesten Beispielen zu quälen. Beginne mit Dreiecken und Vierecken. Wenn du die drauf hast, kannst du dich an komplexere Figuren wagen.

Wie man Aufgaben zur Zentrischen Streckung löst (die einfache Version)

Okay, hier kommt die Kurzfassung, wie man diese Aufgaben knackt:

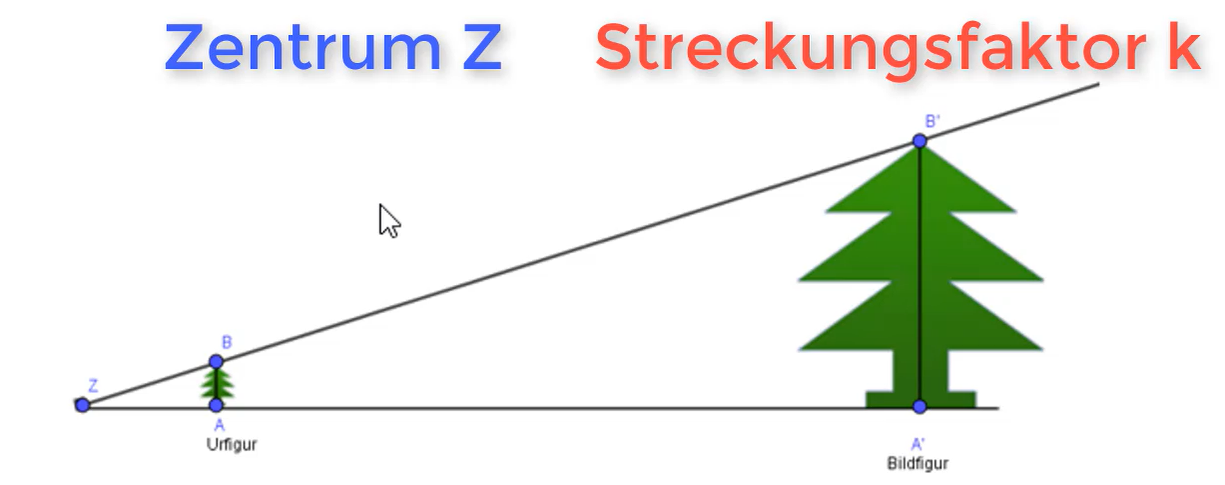
1. Finde das Zentrum: Das ist der Ausgangspunkt für alles!
2. Bestimme den Streckungsfaktor: Dieser Faktor sagt dir, um wie viel größer oder kleiner die Figur wird. Ein Faktor von 2 bedeutet doppelte Größe, ein Faktor von 0,5 halbe Größe.
3. Verbinde: Verbinde das Zentrum mit den Eckpunkten der ursprünglichen Figur.
4. Messe und multipliziere: Miss die Entfernung vom Zentrum zu jedem Eckpunkt. Multipliziere diese Entfernung mit dem Streckungsfaktor.
5. Zeichne: Trage die neuen Punkte (die du durch die Multiplikation erhalten hast) auf den Linien ein und verbinde sie. Fertig!

Klingt kompliziert? Ist es aber nicht! Mit ein bisschen Übung wirst du zum Zentrische-Streckungs-Meister!

Wo bekomme ich diese magischen PDFs?

Googeln ist dein Freund! Such einfach nach "Zentrische Streckung Aufgaben mit Lösungen PDF" und du wirst eine Fülle an Materialien finden. Schau dir verschiedene Quellen an und wähle die, die dir am besten gefallen. Manche sind interaktiver, andere sind eher klassisch. Finde, was für dich am besten passt.

Wichtiger Hinweis: Achte darauf, dass die Lösungen verständlich sind. Es bringt nichts, wenn du die Lösung hast, aber nicht verstehst, wie sie zustande gekommen ist.

Und jetzt?

Jetzt heißt es: Üben, üben, üben! Je mehr Aufgaben du löst, desto besser wirst du darin. Und denk daran: Mathe soll Spaß machen! Wenn es dir zu frustrierend wird, mach eine Pause und komm später wieder. Oder schnapp dir einen Freund und löst die Aufgaben zusammen. Gemeinsam macht's mehr Spaß!

Denk daran: Du bist schlauer, als du denkst. Zentrische Streckung ist kein Hexenwerk. Mit ein bisschen Geduld und Übung wirst du diese Aufgaben im Handumdrehen lösen.

Also, Kopf hoch, Stift in die Hand und los geht's! Du schaffst das!