Berechnung Des Volumens Eines Zylinders

Haben Sie sich jemals gefragt, wie viel Wasser in einen zylindrischen Pool passt? Oder wie viel Farbe Sie benötigen, um eine zylindrische Säule zu streichen? Die Antwort liegt in der Berechnung des Volumens eines Zylinders. Keine Angst, es ist einfacher als es aussieht! Viele Leute empfinden Geometrie als abschreckend, aber mit dieser Anleitung werden wir die Berechnung des Zylindervolumens entmystifizieren und Ihnen das nötige Wissen vermitteln, um diese Aufgabe selbstbewusst zu meistern.

Was ist ein Zylinder?

Bevor wir uns mit der Berechnung befassen, definieren wir zunächst, was ein Zylinder eigentlich ist. Stellen Sie sich eine Konservendose vor oder eine Rolle Küchenpapier. Ein Zylinder ist eine dreidimensionale geometrische Figur mit zwei parallelen, kongruenten (identischen) kreisförmigen Basen, die durch eine gekrümmte Oberfläche verbunden sind. Diese gekrümmte Oberfläche ist das, was die beiden Kreise zu einer geschlossenen Form verbindet. Denken Sie daran: Es hat keine Ecken oder spitzen Winkel!

Die wichtigsten Eigenschaften eines Zylinders sind:

• Grundfläche: Die beiden identischen Kreise an den Enden des Zylinders.
• Radius (r): Der Radius einer der kreisförmigen Grundflächen. Das ist der Abstand vom Mittelpunkt des Kreises zum Rand.
• Höhe (h): Der senkrechte Abstand zwischen den beiden Grundflächen. Stellen Sie sich vor, Sie würden den Zylinder auf eine seiner Grundflächen stellen; die Höhe ist dann die vertikale Distanz vom Boden bis zum Deckel.

Die Formel zur Berechnung des Zylindervolumens

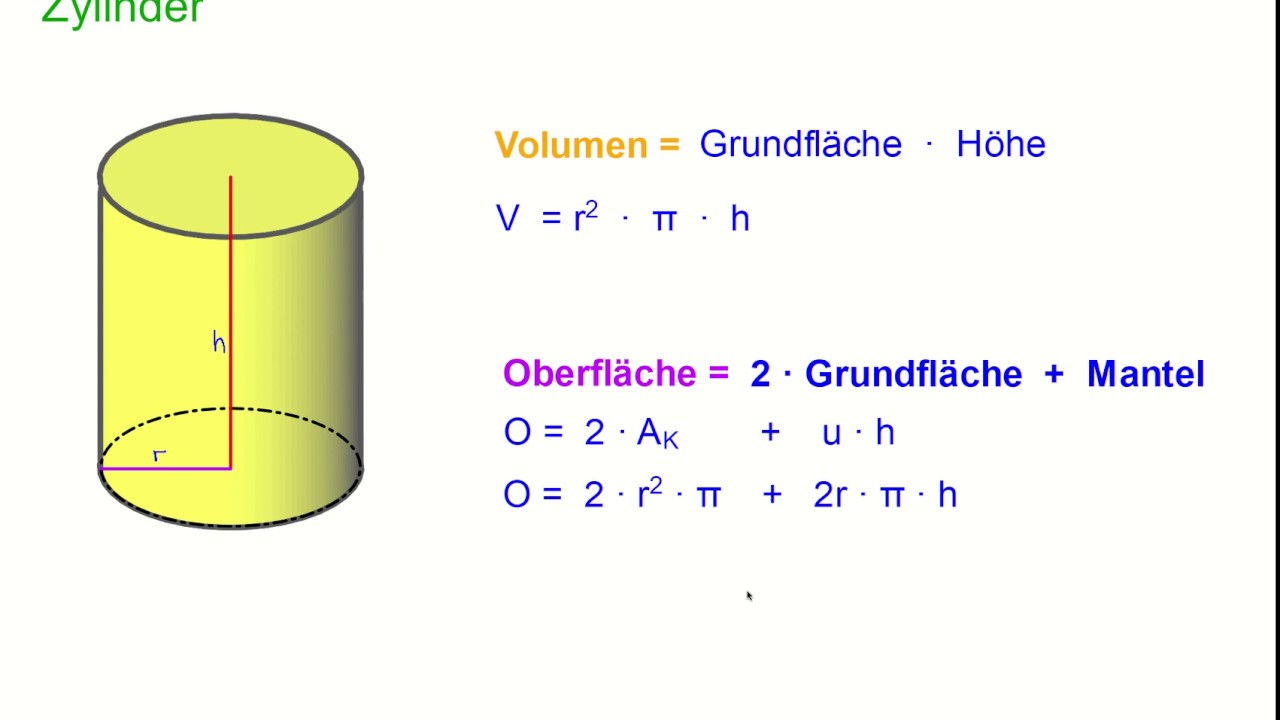
Nun zum Kern der Sache: Wie berechnet man das Volumen eines Zylinders? Die Formel ist überraschend einfach und elegant:

Volumen (V) = π * r² * h

Lassen wir diese Formel aufschlüsseln:

• V: Das Volumen des Zylinders (das, was wir berechnen wollen). Es wird in Kubikeinheiten angegeben (z. B. cm³, m³, in³).
• π (Pi): Eine mathematische Konstante, die ungefähr 3,14159 beträgt. Pi ist das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser. Die meisten Taschenrechner haben eine Pi-Taste, die eine genauere Darstellung von Pi verwendet.
• r: Der Radius einer der kreisförmigen Grundflächen. Denken Sie daran: Wenn Ihnen der Durchmesser gegeben ist, teilen Sie ihn durch 2, um den Radius zu erhalten (Radius = Durchmesser / 2).
• h: Die Höhe des Zylinders.

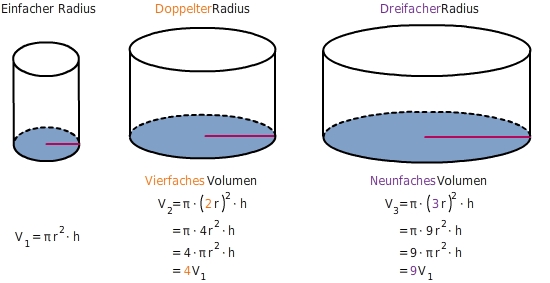
Die Formel sagt im Wesentlichen, dass das Volumen eines Zylinders gleich der Fläche seiner Grundfläche (πr²) multipliziert mit seiner Höhe ist. Denken Sie darüber nach: Sie berechnen im Grunde, wie viele dieser kreisförmigen Grundflächen "gestapelt" werden, um die Höhe des Zylinders zu füllen.

Schritt-für-Schritt-Anleitung zur Berechnung des Zylindervolumens

Lassen Sie uns die Berechnung in eine einfache Schritt-für-Schritt-Anleitung aufteilen:

1. Bestimmen Sie den Radius (r) der kreisförmigen Grundfläche: Wenn der Radius direkt angegeben ist, sind Sie startklar. Wenn Sie den Durchmesser haben, teilen Sie ihn durch 2, um den Radius zu erhalten.
2. Bestimmen Sie die Höhe (h) des Zylinders: Stellen Sie sicher, dass Radius und Höhe in der gleichen Einheit gemessen werden (z. B. beide in Zentimetern oder beide in Metern).
3. Quadrieren Sie den Radius (r²): Multiplizieren Sie den Radius mit sich selbst.
4. Multiplizieren Sie das Ergebnis mit π (Pi): Verwenden Sie entweder 3,14159 oder die Pi-Taste auf Ihrem Taschenrechner für eine genauere Antwort.
5. Multiplizieren Sie das Ergebnis mit der Höhe (h): Dies ergibt das Volumen des Zylinders.
6. Geben Sie die Einheiten an: Das Volumen wird in Kubikeinheiten angegeben. Wenn Radius und Höhe in Zentimetern gemessen wurden, wird das Volumen in Kubikzentimetern (cm³) angegeben. Wenn sie in Metern gemessen wurden, wird das Volumen in Kubikmetern (m³) angegeben usw.

Beispiele zur Berechnung des Zylindervolumens

Lassen Sie uns dies anhand einiger Beispiele veranschaulichen:

Beispiel 1:

Ein Zylinder hat einen Radius von 5 cm und eine Höhe von 10 cm. Berechnen Sie sein Volumen.

1. Radius (r) = 5 cm
2. Höhe (h) = 10 cm
3. r² = 5 cm * 5 cm = 25 cm²
4. π * r² = 3,14159 * 25 cm² = 78,53975 cm²
5. V = π * r² * h = 78,53975 cm² * 10 cm = 785,3975 cm³

Daher beträgt das Volumen des Zylinders 785,3975 cm³.

Beispiel 2:

Ein Zylinder hat einen Durchmesser von 8 Metern und eine Höhe von 12 Metern. Berechnen Sie sein Volumen.

1. Radius (r) = Durchmesser / 2 = 8 m / 2 = 4 m
2. Höhe (h) = 12 m
3. r² = 4 m * 4 m = 16 m²
4. π * r² = 3,14159 * 16 m² = 50,26544 m²
5. V = π * r² * h = 50,26544 m² * 12 m = 603,18528 m³

Daher beträgt das Volumen des Zylinders 603,18528 m³.

Beispiel 3: (Praktisches Beispiel)

Sie möchten einen zylindrischen Behälter mit Wasser füllen. Der Behälter hat einen Radius von 15 cm und eine Höhe von 30 cm. Wie viel Wasser benötigen Sie in Litern?

1. Radius (r) = 15 cm
2. Höhe (h) = 30 cm
3. r² = 15 cm * 15 cm = 225 cm²
4. π * r² = 3,14159 * 225 cm² = 706,85775 cm²
5. V = π * r² * h = 706,85775 cm² * 30 cm = 21205,7325 cm³

Das Volumen des Behälters beträgt 21205,7325 cm³. Um dies in Liter umzurechnen, verwenden wir die Tatsache, dass 1 Liter = 1000 cm³.

Volumen in Litern = 21205,7325 cm³ / 1000 cm³/Liter = 21,2057325 Liter

Daher benötigen Sie ungefähr 21,21 Liter Wasser, um den Behälter zu füllen. (Auf zwei Dezimalstellen gerundet).

Häufige Fehler, die Sie vermeiden sollten

Hier sind einige häufige Fehler, die Menschen bei der Berechnung des Zylindervolumens machen und wie Sie sie vermeiden können:

• Verwendung des Durchmessers anstelle des Radius: Denken Sie daran: Die Formel verwendet den Radius (r), nicht den Durchmesser. Wenn Ihnen der Durchmesser gegeben ist, teilen Sie ihn immer durch 2, um den Radius zu erhalten.
• Falsche Einheiten: Stellen Sie sicher, dass Radius und Höhe in den gleichen Einheiten gemessen werden. Wenn sie nicht gleich sind, müssen Sie eine der Messungen umrechnen, bevor Sie die Formel anwenden. Zum Beispiel, wenn der Radius in Zentimetern und die Höhe in Metern angegeben ist, wandeln Sie die Höhe in Zentimeter oder den Radius in Meter um.
• Vergessen der Kubikeinheiten: Das Volumen wird immer in Kubikeinheiten angegeben (z. B. cm³, m³, in³). Vergessen Sie nicht, die richtigen Einheiten am Ende Ihrer Berechnung anzugeben.
• Falsche Eingabe in den Taschenrechner: Überprüfen Sie Ihre Eingaben sorgfältig, besonders bei der Verwendung der Pi-Taste. Ein kleiner Fehler kann zu einer großen Abweichung im Ergebnis führen.

Warum ist die Berechnung des Zylindervolumens wichtig?

Die Berechnung des Zylindervolumens hat viele praktische Anwendungen im Alltag und in verschiedenen Berufen:

• Ingenieurwesen: Ingenieure verwenden die Berechnung des Zylindervolumens, um die Kapazität von Rohren, Tanks und anderen zylindrischen Strukturen zu bestimmen.
• Architektur: Architekten nutzen diese Berechnungen, um das Volumen von zylindrischen Säulen, Behältern oder anderen architektonischen Elementen zu bestimmen.
• Fertigung: In der Fertigung wird das Zylindervolumen verwendet, um die Materialmenge zu berechnen, die zur Herstellung zylindrischer Produkte wie Dosen, Rohre und Behälter benötigt wird.
• Medizin: In der Medizin kann die Volumenberechnung für die Dosierung von Medikamenten in Spritzen oder die Berechnung des Blutvolumens in Blutgefäßen verwendet werden.
• Kochen und Backen: Im Alltag kann die Berechnung des Zylindervolumens hilfreich sein, um die Kapazität von Backformen, Tassen oder anderen zylindrischen Messbehältern zu bestimmen.
• Landwirtschaft: Landwirte verwenden die Berechnung des Zylindervolumens, um das Fassungsvermögen von Silos zur Getreidelagerung zu bestimmen.

Kurz gesagt, das Verständnis der Berechnung des Zylindervolumens ist eine wertvolle Fähigkeit mit vielfältigen Anwendungen.

Alternative Methoden und Werkzeuge

Obwohl die Formel V = π * r² * h die gebräuchlichste und effizienteste Methode zur Berechnung des Zylindervolumens ist, gibt es alternative Methoden und Werkzeuge, die verwendet werden können:

• Online-Rechner: Es gibt zahlreiche Online-Rechner, die speziell für die Berechnung des Zylindervolumens entwickelt wurden. Sie müssen lediglich den Radius und die Höhe eingeben, und der Rechner liefert Ihnen das Ergebnis. Diese Rechner sind besonders nützlich, wenn Sie schnell eine Berechnung durchführen müssen oder wenn Sie sich der Genauigkeit Ihrer eigenen Berechnung nicht sicher sind.
• CAD-Software (Computer-Aided Design): CAD-Software wird häufig in der Architektur und im Ingenieurwesen verwendet. Sie kann verwendet werden, um 3D-Modelle von Zylindern zu erstellen und automatisch das Volumen zu berechnen.
• Experimentelle Methoden: In einigen Fällen, insbesondere wenn es sich um unregelmäßig geformte Zylinder handelt, kann das Volumen experimentell durch Eintauchen des Zylinders in einen Behälter mit bekanntem Volumen an Wasser und Messen der Wasserverdrängung bestimmt werden. Dies wird als Archimedes' Prinzip bezeichnet.

Fazit

Die Berechnung des Zylindervolumens ist eine grundlegende, aber wichtige Fähigkeit mit breiten Anwendungsmöglichkeiten. Indem Sie die Definition eines Zylinders, die Formel V = π * r² * h und die schrittweise Anleitung verstehen, können Sie das Volumen eines jeden Zylinders selbstbewusst und genau berechnen. Vermeiden Sie die häufigsten Fehler und nutzen Sie bei Bedarf alternative Methoden und Werkzeuge. Mit Übung werden Sie feststellen, dass die Berechnung des Zylindervolumens eine einfache und lohnende Aufgabe ist.

Also, das nächste Mal, wenn Sie sich fragen, wie viel Farbe Sie für diese zylindrische Säule benötigen oder wie viel Wasser in Ihren zylindrischen Pool passt, wissen Sie, was zu tun ist! Viel Spaß beim Rechnen!