Berechnung Einer Diagonalen Im Rechteck

Stell dir vor, du sitzt vor einer Aufgabe und musst die Länge einer Diagonalen in einem Rechteck berechnen. Vielleicht bastelst du etwas, planst ein Zimmer oder hilfst deinem Kind bei den Hausaufgaben. Die Berechnung kann erstmal kompliziert erscheinen, aber keine Sorge, es ist einfacher als du denkst! Viele denken, Mathematik ist trocken und unnütz, aber die Berechnung von Diagonalen ist überraschend praxisnah und hilft dir in vielen Alltagssituationen.

Warum ist das überhaupt wichtig?

Vielleicht fragst du dich, warum du die Diagonale eines Rechtecks überhaupt berechnen solltest. Hier ein paar Beispiele, wo diese Fähigkeit nützlich sein kann:

• Bauprojekte: Um sicherzustellen, dass ein rechteckiger Raum oder eine Fläche wirklich rechteckig ist. Eine ungenaue Diagonale deutet auf einen Winkel ungleich 90 Grad hin.
• Basteln: Beim Zuschneiden von Stoffen oder Papier für kreative Projekte.
• Navigation: Um die direkte Entfernung zwischen zwei Punkten zu berechnen, wenn du nur die horizontalen und vertikalen Entfernungen kennst.
• Computergrafik: Bei der Berechnung von Distanzen und Winkeln in 2D-Grafiken.

Du siehst, die Berechnung einer Diagonale ist nicht nur eine abstrakte mathematische Übung, sondern hat direkte Auswirkungen auf unsere Lebensqualität. Denk nur daran, wenn du das nächste Mal ein Regal baust oder ein Bild aufhängst!

Die Herausforderung verstehen

Viele Leute haben Schwierigkeiten mit Mathematik, weil sie sich nicht vorstellen können, wie die Konzepte in der realen Welt angewendet werden. Die Formeln wirken abstrakt und einschüchternd. Außerdem ist es leicht, sich in den Details zu verlieren und den Überblick zu verlieren, warum man das Ganze überhaupt macht. Einige argumentieren, dass solche Berechnungen heutzutage unnötig sind, da es Apps und Rechner gibt, die diese Aufgaben übernehmen können. Allerdings ist das Verständnis der dahinterliegenden Prinzipien wichtig, um die Ergebnisse zu interpretieren und Fehler zu erkennen.

Wir werden das Problem daher schrittweise angehen und sicherstellen, dass du nicht nur die Formel kennst, sondern auch verstehst, warum sie funktioniert.

Die Lösung: Der Satz des Pythagoras

Die wichtigste Grundlage für die Berechnung der Diagonale eines Rechtecks ist der Satz des Pythagoras. Vielleicht hast du ihn schon mal gehört, aber lass uns ihn kurz wiederholen:

In einem rechtwinkligen Dreieck (ein Dreieck mit einem 90-Grad-Winkel) ist das Quadrat der Hypotenuse (der Seite gegenüber dem rechten Winkel) gleich der Summe der Quadrate der beiden anderen Seiten (Katheten).

Mathematisch ausgedrückt:

a² + b² = c²

Wobei:

• a und b die Längen der Katheten sind.
• c die Länge der Hypotenuse ist.

Wie hängt das mit dem Rechteck zusammen?

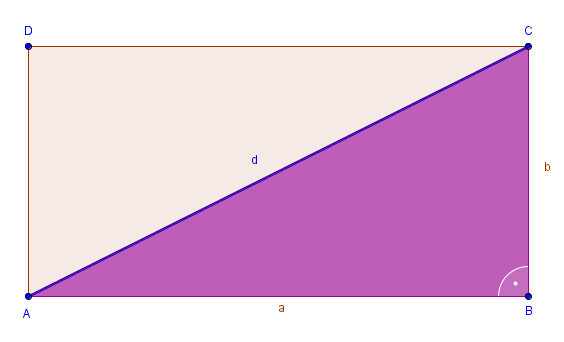
Die Diagonale eines Rechtecks teilt dieses in zwei rechtwinklige Dreiecke. Die Seiten des Rechtecks sind die Katheten (a und b) und die Diagonale ist die Hypotenuse (c).

Das bedeutet, wir können den Satz des Pythagoras verwenden, um die Länge der Diagonale zu berechnen!

Die Formel zur Berechnung der Diagonale

Um die Länge der Diagonale (d) eines Rechtecks mit den Seitenlängen a und b zu berechnen, verwenden wir folgende Formel:

d = √(a² + b²)

Das bedeutet:

1. Quadriere die Länge der einen Seite (a²).
2. Quadriere die Länge der anderen Seite (b²).
3. Addiere die beiden Quadrate (a² + b²).
4. Ziehe die Quadratwurzel aus der Summe (√(a² + b²)). Das Ergebnis ist die Länge der Diagonale.

Ein einfaches Beispiel

Nehmen wir an, ein Rechteck hat eine Länge von 4 cm (a) und eine Breite von 3 cm (b). Wie lang ist die Diagonale?

1. a² = 4² = 16
2. b² = 3² = 9
3. a² + b² = 16 + 9 = 25
4. √(a² + b²) = √25 = 5

Die Diagonale ist also 5 cm lang.

Schritt-für-Schritt-Anleitung

1. Miss die Länge und Breite des Rechtecks. Achte darauf, dass du die gleichen Einheiten verwendest (z.B. Zentimeter, Meter, Zoll).
2. Quadriere die Länge und die Breite. Multipliziere jede Zahl mit sich selbst.
3. Addiere die beiden Quadrate.
4. Ziehe die Quadratwurzel der Summe. Du kannst einen Taschenrechner oder eine Quadratwurzeltabelle verwenden, um die Quadratwurzel zu finden.
5. Das Ergebnis ist die Länge der Diagonale. Gib die Einheit an, in der du gemessen hast.

Komplexere Beispiele und Variationen

Was, wenn du die Diagonale und eine Seite kennst, aber die andere Seite berechnen musst? Kein Problem! Du kannst den Satz des Pythagoras umstellen:

Wenn du die Diagonale (d) und die Seite a kennst, dann ist:

b = √(d² - a²)

Wenn du die Diagonale (d) und die Seite b kennst, dann ist:

a = √(d² - b²)

Auch hier gilt: Quadriere die bekannten Werte, subtrahiere sie und ziehe die Quadratwurzel, um die fehlende Seite zu berechnen.

Beispiel für eine Umstellung

Ein Rechteck hat eine Diagonale von 13 cm und eine Seite von 5 cm. Wie lang ist die andere Seite?

a = 5 cm

d = 13 cm

b = √(d² - a²) = √(13² - 5²) = √(169 - 25) = √144 = 12

Die andere Seite ist also 12 cm lang.

Typische Fehler vermeiden

Hier sind ein paar häufige Fehler, die du vermeiden solltest:

• Einheiten vergessen: Achte immer darauf, die Einheiten anzugeben (z.B. cm, m, Zoll).
• Falsche Quadrierung: Überprüfe, ob du die Zahlen richtig quadriert hast (z.B. 4² = 4 * 4 = 16, nicht 4 * 2 = 8).
• Falsche Formel: Verwende immer die korrekte Formel für die Berechnung der Diagonale oder der fehlenden Seite.
• Fehler beim Wurzelziehen: Benutze einen Taschenrechner, um Fehler beim Ziehen der Quadratwurzel zu vermeiden.
• Falsche Anwendung des Satzes des Pythagoras: Vergewissere dich, dass du die Hypotenuse und die Katheten richtig identifiziert hast.

Alternative Methoden

Obwohl der Satz des Pythagoras die gebräuchlichste Methode ist, gibt es in speziellen Fällen auch andere Ansätze. Wenn du beispielsweise mit ähnlichen Dreiecken arbeitest, kannst du Proportionen verwenden, um die Länge der Diagonale zu bestimmen. Diese Methode ist jedoch in der Regel komplexer und erfordert ein tieferes Verständnis der Geometrie.

Es gibt auch Online-Rechner, die die Diagonale automatisch berechnen. Diese sind zwar praktisch, aber sie helfen dir nicht, das Konzept zu verstehen. Es ist wichtig, die Grundlagen zu beherrschen, bevor du dich auf Tools verlässt.

Zusammenfassung und wichtige Erkenntnisse

Die Berechnung der Diagonale eines Rechtecks ist eine nützliche Fähigkeit, die auf dem Satz des Pythagoras basiert. Mit der Formel d = √(a² + b²) kannst du die Länge der Diagonale einfach und schnell berechnen.

Denke daran, die Einheiten anzugeben, die Zahlen richtig zu quadrieren und die Quadratwurzel korrekt zu ziehen. Wenn du diese Schritte befolgst, kannst du Fehler vermeiden und genaue Ergebnisse erzielen.

Dieses Wissen ist nicht nur für mathematische Aufgaben wichtig, sondern auch für praktische Anwendungen im Alltag, wie z.B. Bauprojekte, Basteln und Navigation.

Nächste Schritte

Jetzt, da du die Grundlagen verstanden hast, versuche dich an ein paar Übungsaufgaben. Nimm dir ein Lineal und miss die Seiten verschiedener rechteckiger Objekte in deinem Zuhause. Berechne dann die Länge der Diagonalen und überprüfe dein Ergebnis mit einem Taschenrechner oder einem Online-Rechner.

Versuche auch, komplexere Aufgaben zu lösen, bei denen du die Diagonale und eine Seite kennst und die andere Seite berechnen musst.

Indem du übst, wirst du sicherer im Umgang mit der Formel und kannst sie in verschiedenen Situationen anwenden.

Wie fühlst du dich jetzt mit der Berechnung der Diagonale im Rechteck? Bist du bereit, dein neues Wissen in die Praxis umzusetzen und ein eigenes Projekt zu starten?