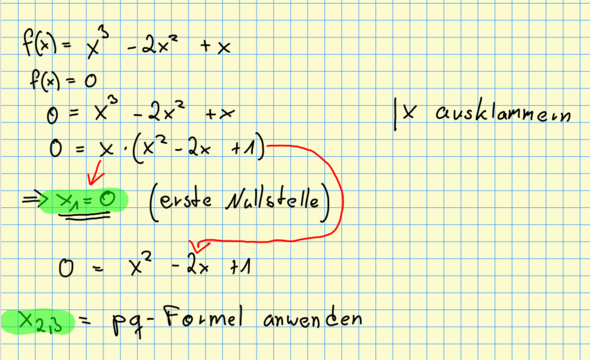Nullstellen Funktion 3 Grades Berechnen

Nullstellen von Funktionen 3. Grades: Ein Leitfaden für Lehrkräfte
Die Bestimmung der Nullstellen von Funktionen 3. Grades ist ein Kernbestandteil des Mathematikunterrichts. Es ist ein Thema, das Schüler oft vor Herausforderungen stellt. Dieser Artikel bietet Ihnen einen Leitfaden, um diese Herausforderungen zu meistern und den Unterricht effektiver zu gestalten. Denken Sie daran, die Schüler aktiv einzubeziehen.
Funktionen 3. Grades haben die allgemeine Form f(x) = ax³ + bx² + cx + d, wobei a, b, c und d Konstanten sind und a ≠ 0 gilt. Die Nullstellen sind die Werte von x, für die f(x) = 0 ist. Eine Funktion 3. Grades hat immer mindestens eine reelle Nullstelle und höchstens drei.
Methoden zur Berechnung
Es gibt verschiedene Methoden, um die Nullstellen zu berechnen. Die Wahl der Methode hängt von der spezifischen Form der Funktion ab. Die einfachsten Fälle lassen sich durch Ausklammern und Faktorisieren lösen.
1. Ausklammern: Manchmal kann man einen gemeinsamen Faktor aus allen Termen ausklammern. Das vereinfacht die Gleichung. Betrachten Sie zum Beispiel f(x) = x³ + 2x² + x. Hier können Sie x ausklammern: f(x) = x(x² + 2x + 1). Die Nullstellen sind dann x = 0 und die Lösungen der quadratischen Gleichung x² + 2x + 1 = 0.
2. Faktorisieren: Versuchen Sie, die Funktion in Faktoren zu zerlegen. Dies kann durch systematisches Ausprobieren oder durch Anwendung spezieller Faktorisierungstechniken geschehen. Dies ist besonders nützlich, wenn man eine Nullstelle bereits kennt (z.B. durch Raten oder aus dem Kontext der Aufgabe).
3. Raten einer Nullstelle und Polynomdivision: Dies ist eine wichtige Methode. Wenn Sie eine Nullstelle x₁ gefunden haben, können Sie die Funktion durch (x - x₁) dividieren. Das Ergebnis ist eine quadratische Funktion, deren Nullstellen sich mit der quadratischen Lösungsformel (Mitternachtsformel) bestimmen lassen. Die gefundene Nullstelle kann durch systematisches Einsetzen kleiner ganzer Zahlen (z.B. -2, -1, 0, 1, 2) erraten werden.
4. Cardanische Formeln: Diese Formeln sind ein allgemeiner Ansatz. Sie sind allerdings komplex und für den Schulunterricht oft ungeeignet. Sie liefern die exakten Lösungen, sind aber rechenintensiv.
Tipps für den Unterricht
Beginnen Sie mit einfachen Beispielen. Arbeiten Sie sich dann zu komplexeren Aufgaben vor. Dies hilft den Schülern, ein solides Fundament zu entwickeln. Visualisierungen, wie Graphen der Funktionen, sind sehr hilfreich. Verwenden Sie Geogebra oder ähnliche Tools, um die Funktionen darzustellen und die Nullstellen zu veranschaulichen. Betonen Sie die Verbindung zwischen den Nullstellen und den Schnittpunkten des Graphen mit der x-Achse.
Bieten Sie eine Vielzahl von Übungsaufgaben an. Diese sollten unterschiedliche Schwierigkeitsgrade haben. Ermutigen Sie die Schüler, ihre Lösungswege zu erklären. Dies fördert das Verständnis und die Problemlösungsfähigkeiten. Gruppenarbeit kann auch sehr effektiv sein. Die Schüler können sich gegenseitig helfen und voneinander lernen.
Häufige Missverständnisse
Ein häufiges Missverständnis ist, dass Funktionen 3. Grades immer drei reelle Nullstellen haben. Das ist nicht der Fall. Sie können auch nur eine reelle Nullstelle und zwei konjugiert komplexe Nullstellen haben. Ein weiteres Missverständnis ist, dass die Polynomdivision immer einfach ist. Manchmal ist sie knifflig und erfordert sorgfältige Arbeit. Schüler verwechseln oft die Begriffe Nullstelle und Extremstelle. Machen Sie den Unterschied klar.
Wie man das Thema ansprechend gestaltet
Verbinden Sie das Thema mit realen Anwendungen. Funktionen 3. Grades können z.B. verwendet werden, um Volumen oder Wachstumsraten zu modellieren. Verwenden Sie interaktive Tools und Simulationen. Diese können das Lernen spannender gestalten. Stellen Sie Aufgaben, die die Kreativität der Schüler fördern. Zum Beispiel können sie eigene Funktionen entwerfen, die bestimmte Nullstellen haben.
Motivieren Sie die Schüler, Fragen zu stellen. Schaffen Sie eine offene und unterstützende Lernumgebung. Geben Sie konstruktives Feedback. Dies hilft den Schülern, ihre Fehler zu erkennen und zu korrigieren. Feiern Sie Erfolge. Dies stärkt das Selbstvertrauen der Schüler.
Die Bestimmung der Nullstellen von Funktionen 3. Grades ist eine wichtige Fähigkeit. Mit den richtigen Methoden und einer klaren Vermittlung können Sie Ihren Schülern helfen, dieses Thema zu meistern. Denken Sie daran, geduldig zu sein und die Schüler zu ermutigen. Viel Erfolg beim Unterrichten!