Satz Von Der Totalen Wahrscheinlichkeit

Einführung in den Satz von der totalen Wahrscheinlichkeit
Stell dir vor, du bist ein Detektiv. Du versuchst, ein Rätsel zu lösen. Dieses Rätsel hat viele Teile. Der Satz von der totalen Wahrscheinlichkeit hilft dir, das große Ganze zu verstehen, indem er die einzelnen Teile zusammenfügt.
Es ist wie ein Puzzle. Jedes Puzzleteil ist ein kleines Ereignis. Der Satz von der totalen Wahrscheinlichkeit hilft dir, die Wahrscheinlichkeit eines großen Ereignisses zu finden, indem du die Wahrscheinlichkeiten der einzelnen Puzzleteile betrachtest.
Was ist der Satz von der totalen Wahrscheinlichkeit?
Der Satz von der totalen Wahrscheinlichkeit ist ein mathematisches Werkzeug. Es hilft uns, die Wahrscheinlichkeit eines Ereignisses zu berechnen. Dafür betrachten wir verschiedene, sich gegenseitig ausschließende Szenarien.
Denk an einen Kuchen. Du schneidest ihn in Stücke. Jedes Stück ist ein Szenario. Die Wahrscheinlichkeit, ein bestimmtes Stück zu bekommen (ein bestimmtes Ereignis), hängt davon ab, wie groß jedes Stück ist und wie wahrscheinlich es ist, überhaupt ein Stück zu bekommen.
Eine einfache Analogie: Die Wettervorhersage
Angenommen, es gibt zwei Nachrichtenquellen für das Wetter. Quelle A sagt mit 70% Wahrscheinlichkeit Regen voraus. Quelle B sagt mit 30% Wahrscheinlichkeit Regen voraus. Du vertraust Quelle A zu 60% und Quelle B zu 40%.
Was ist die Wahrscheinlichkeit, dass es regnet? Der Satz von der totalen Wahrscheinlichkeit hilft uns, diese Frage zu beantworten. Wir müssen die Wahrscheinlichkeit für Regen aus beiden Quellen berücksichtigen, gewichtet nach unserem Vertrauen in jede Quelle.
Die Berechnung sieht so aus: (Wahrscheinlichkeit Regen von A * Vertrauen in A) + (Wahrscheinlichkeit Regen von B * Vertrauen in B) = (0.7 * 0.6) + (0.3 * 0.4) = 0.42 + 0.12 = 0.54. Also beträgt die totale Wahrscheinlichkeit für Regen 54%.
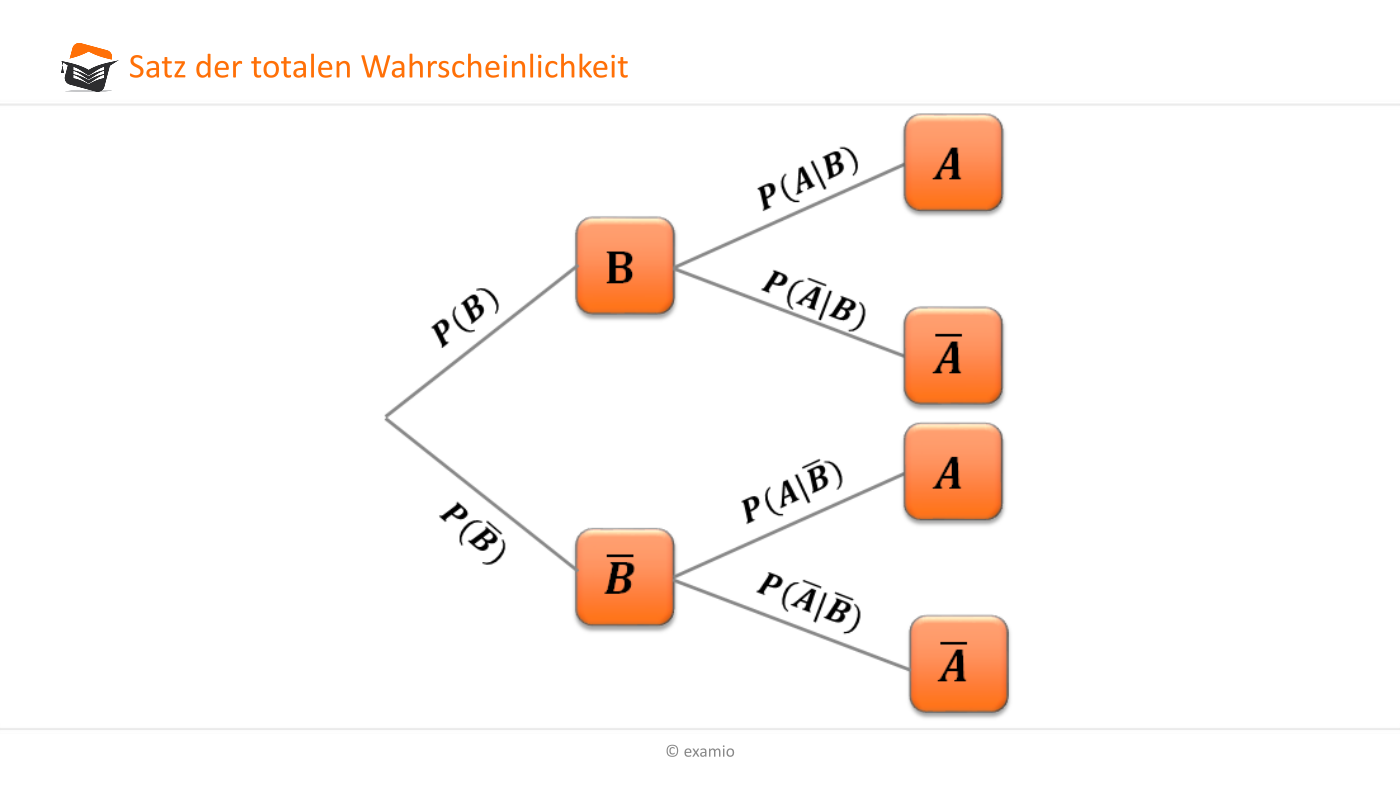
Wie funktioniert es visuell?
Stell dir ein großes Rechteck vor. Dieses Rechteck repräsentiert alle möglichen Ergebnisse. Teile dieses Rechteck in kleinere, nicht überlappende Rechtecke auf. Jedes kleinere Rechteck repräsentiert ein Szenario.
Innerhalb jedes kleinen Rechtecks befindet sich ein Bereich, der das Ereignis repräsentiert, an dem wir interessiert sind. Die Größe dieses Bereichs relativ zum Gesamtbereich des kleinen Rechtecks repräsentiert die Wahrscheinlichkeit des Ereignisses, *gegeben*, dass dieses Szenario eintritt.
Um die totale Wahrscheinlichkeit des Ereignisses zu finden, berechnen wir die Fläche des Ereignisses *in jedem* kleinen Rechteck. Dann addieren wir diese Flächen zusammen. Das ergibt uns die Gesamtfläche, die das Ereignis in allen Szenarien repräsentiert.
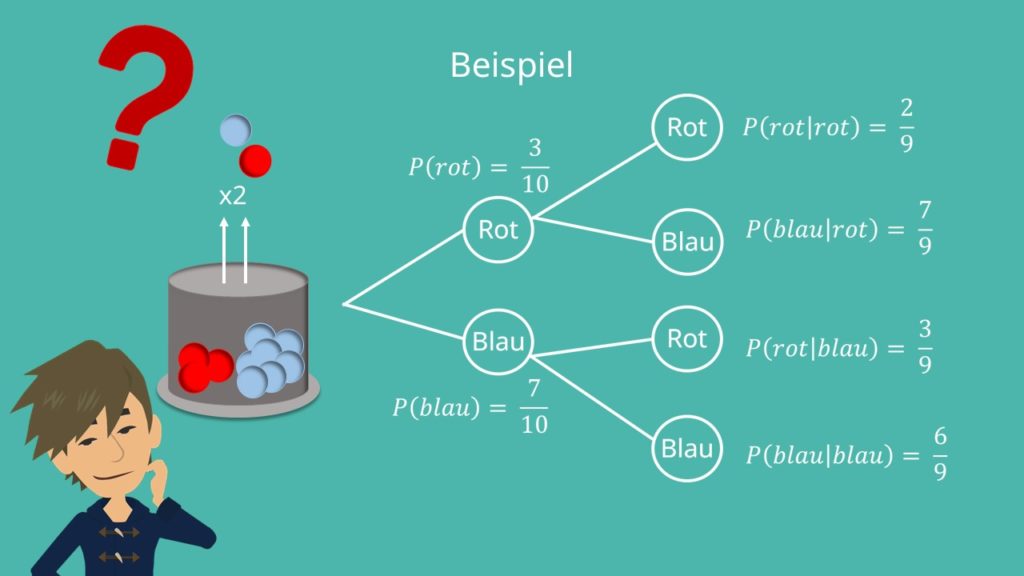
Ein weiteres Beispiel: Kugeln in Urnen
Stell dir vor, du hast zwei Urnen. Urne 1 enthält 6 rote und 4 blaue Kugeln. Urne 2 enthält 3 rote und 7 blaue Kugeln. Du wählst zufällig eine Urne aus und ziehst dann eine Kugel.
Was ist die Wahrscheinlichkeit, dass du eine rote Kugel ziehst? Um das herauszufinden, musst du die Wahrscheinlichkeit berücksichtigen, jede Urne auszuwählen (normalerweise 50% für jede). Dann berücksichtigst du die Wahrscheinlichkeit, eine rote Kugel zu ziehen, *gegeben* die Urne, die du ausgewählt hast.
Die Wahrscheinlichkeit, Urne 1 zu wählen und eine rote Kugel zu ziehen, ist (0.5 * 0.6) = 0.3. Die Wahrscheinlichkeit, Urne 2 zu wählen und eine rote Kugel zu ziehen, ist (0.5 * 0.3) = 0.15. Die totale Wahrscheinlichkeit, eine rote Kugel zu ziehen, ist also 0.3 + 0.15 = 0.45.
Warum ist das nützlich?
Der Satz von der totalen Wahrscheinlichkeit ist in vielen Bereichen nützlich. Er hilft uns bei der Entscheidungsfindung. Er hilft uns, Risiken zu bewerten. Er hilft uns, komplexe Probleme zu analysieren.
Denk an Medizin. Ein Arzt verwendet den Satz von der totalen Wahrscheinlichkeit, um die Wahrscheinlichkeit einer Krankheit zu berechnen. Er berücksichtigt verschiedene Faktoren, wie z.B. Symptome, Risikofaktoren und Testergebnisse. Dies hilft ihm, eine Diagnose zu stellen und die beste Behandlung zu wählen.
Oder denk an das Finanzwesen. Ein Investor verwendet den Satz von der totalen Wahrscheinlichkeit, um die Wahrscheinlichkeit eines Gewinns oder Verlusts zu berechnen. Er berücksichtigt verschiedene Szenarien, wie z.B. die Entwicklung des Aktienmarktes, die Zinsen und die Inflation. Dies hilft ihm, fundierte Anlageentscheidungen zu treffen.
Zusammenfassung
Der Satz von der totalen Wahrscheinlichkeit ist ein mächtiges Werkzeug. Er hilft uns, komplexe Wahrscheinlichkeiten zu berechnen. Er zerlegt ein Problem in kleinere, handlichere Teile. Dann kombiniert er die Wahrscheinlichkeiten dieser Teile. Dadurch erhalten wir die Wahrscheinlichkeit des großen Ganzen.
Indem du dir den Satz von der totalen Wahrscheinlichkeit als ein Puzzle, einen Kuchen oder verschiedene Pfade vorstellst, kannst du die zugrundeliegenden Prinzipien besser verstehen. Übe mit verschiedenen Beispielen. Bald wirst du in der Lage sein, den Satz von der totalen Wahrscheinlichkeit selbstbewusst anzuwenden.