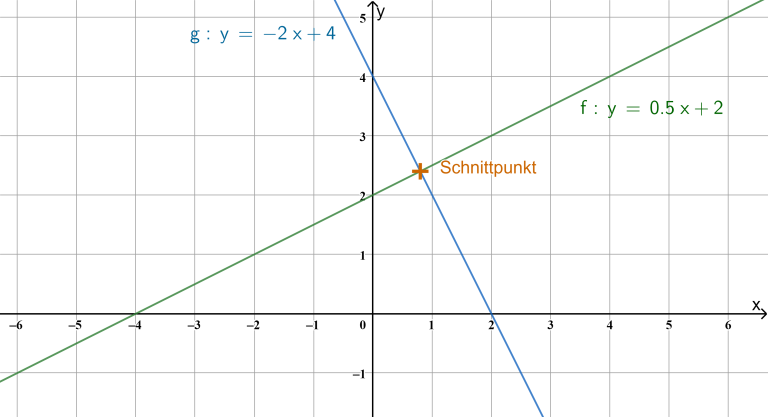
Schnittpunkt Von Zwei Geraden Berechnen

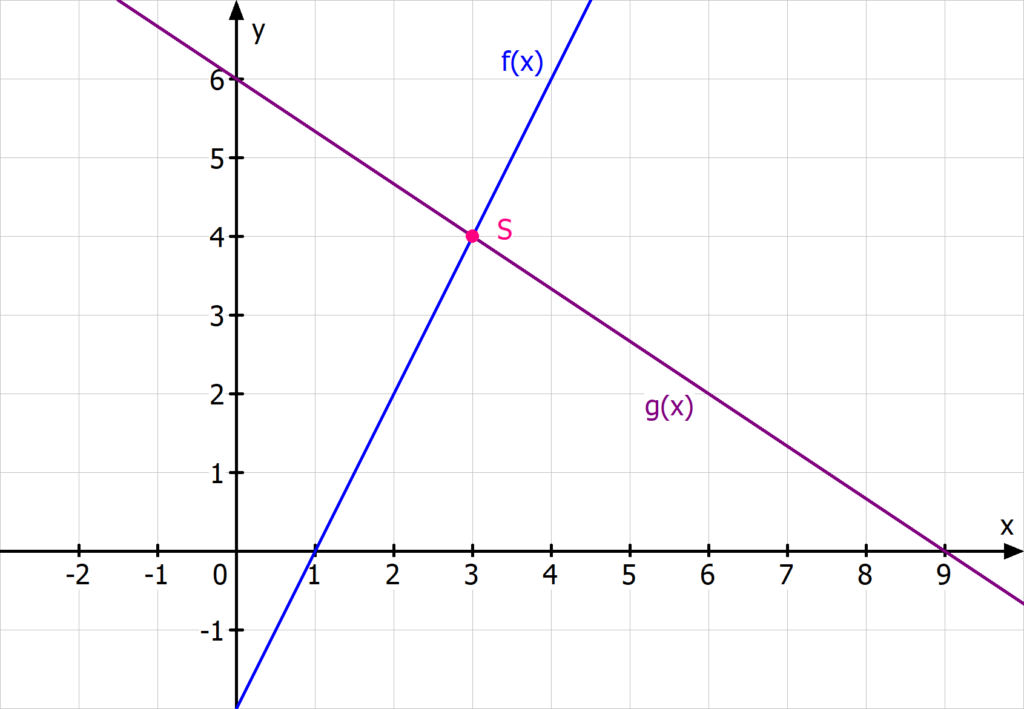
Schnittpunkt zweier Geraden berechnen: Ein Leitfaden für Lehrkräfte

Das Berechnen des Schnittpunkts zweier Geraden ist ein zentrales Thema in der Algebra. Es verknüpft verschiedene mathematische Konzepte. Diese Konzepte sind Gleichungen, Funktionen und geometrische Darstellungen.

Dieser Artikel soll Ihnen helfen, dieses Thema effektiv zu vermitteln. Wir geben Ihnen Tipps für den Unterricht. Wir behandeln gängige Missverständnisse. Wir schlagen Möglichkeiten vor, den Unterricht ansprechender zu gestalten.

Methoden zur Berechnung des Schnittpunkts

Es gibt verschiedene Methoden, um den Schnittpunkt zweier Geraden zu berechnen. Die gängigsten sind das Gleichsetzungsverfahren, das Einsetzungsverfahren und das Additionsverfahren. Wählen Sie die Methode, die am besten zu den gegebenen Gleichungen passt. Es ist wichtig, dass Schüler die Vor- und Nachteile jeder Methode verstehen.

Gleichsetzungsverfahren

Beim Gleichsetzungsverfahren werden beide Gleichungen nach derselben Variablen aufgelöst. Anschließend werden die resultierenden Ausdrücke gleichgesetzt. Dies führt zu einer Gleichung mit einer Variablen, die gelöst werden kann. Setzen Sie den Wert in eine der ursprünglichen Gleichungen ein. So erhalten Sie den Wert der anderen Variablen.

Einsetzungsverfahren

Beim Einsetzungsverfahren wird eine Gleichung nach einer Variablen aufgelöst. Anschließend wird der resultierende Ausdruck in die andere Gleichung eingesetzt. Dies führt zu einer Gleichung mit einer Variablen. Diese kann dann gelöst werden. Setzen Sie den Wert in eine der ursprünglichen Gleichungen ein. So erhalten Sie den Wert der anderen Variablen.

Additionsverfahren (auch Eliminationsverfahren genannt)

Beim Additionsverfahren werden die Gleichungen so manipuliert, dass die Koeffizienten einer Variablen entgegengesetzte Vorzeichen haben. Anschließend werden die Gleichungen addiert. Eine Variable wird dadurch eliminiert. Die resultierende Gleichung kann gelöst werden. Setzen Sie den Wert in eine der ursprünglichen Gleichungen ein. So erhalten Sie den Wert der anderen Variablen.

Tipps für den Unterricht

Beginnen Sie mit einfachen Beispielen. Steigern Sie dann allmählich den Schwierigkeitsgrad. Verwenden Sie grafische Darstellungen. So visualisieren Sie den Schnittpunkt. Fördern Sie die Diskussion im Unterricht. So können Schüler ihre Lösungsansätze austauschen.

Verwenden Sie reale Beispiele. Das macht das Thema relevanter. Beispiele könnten die Berechnung des Treffpunkts zweier Wanderwege sein. Oder die Bestimmung des Punktes, an dem sich Angebot und Nachfrage ausgleichen. Bieten Sie ausreichend Übungsmaterial an. So festigen die Schüler ihr Verständnis.

Lassen Sie die Schüler eigene Aufgaben erstellen. Das fördert ein tieferes Verständnis des Themas. Verwenden Sie interaktive Tools und Software. Diese helfen bei der Visualisierung und beim Lösen von Aufgaben. Beziehen Sie verschiedene Lernstile mit ein. So erreichen Sie alle Schüler.

Gängige Missverständnisse

Ein häufiges Missverständnis ist die Verwechslung von parallelen und identischen Geraden. Parallele Geraden haben keine Schnittpunkte. Identische Geraden haben unendlich viele Schnittpunkte. Klären Sie, dass ein Schnittpunkt ein einzelner Punkt ist.

Schüler haben oft Schwierigkeiten mit negativen Vorzeichen. Auch das korrekte Auflösen von Gleichungen bereitet Probleme. Betonen Sie die Bedeutung von sorgfältiger Arbeit. Üben Sie das Lösen von Gleichungen. Ermutigen Sie die Schüler, ihre Ergebnisse zu überprüfen.

Manche Schüler verstehen nicht, warum man verschiedene Methoden verwenden kann. Erklären Sie, dass alle Methoden zum gleichen Ergebnis führen. Zeigen Sie, wie man die beste Methode für eine bestimmte Aufgabe auswählt. Diskutieren Sie die Effizienz verschiedener Methoden.

Den Unterricht ansprechender gestalten

Verwenden Sie Spiele und Wettbewerbe. Das macht das Lernen spielerischer. Zum Beispiel ein Spiel, bei dem Schüler so schnell wie möglich Schnittpunkte berechnen. Oder eine Schnitzeljagd, bei der die Koordinaten des Schnittpunkts Hinweise liefern.

Lassen Sie die Schüler Präsentationen halten. Das fördert das selbstständige Lernen. Verwenden Sie Technologie. Zum Beispiel GeoGebra, um Geraden zu visualisieren. Nutzen Sie Fallstudien. So zeigen Sie, wie das Thema in der Praxis angewendet wird.

Integrieren Sie das Thema in andere Fächer. Zum Beispiel in Physik oder Wirtschaft. Das zeigt den Schülern die Relevanz des Themas. Ermutigen Sie die Schüler, Fragen zu stellen. Schaffen Sie eine positive Lernumgebung.

"Mathematik ist nicht nur das Lösen von Gleichungen, sondern auch das Verstehen der Welt um uns herum."

Durch die Anwendung dieser Tipps und Strategien können Sie den Schülern helfen, das Berechnen des Schnittpunkts zweier Geraden besser zu verstehen. Sie lernen auch, die Bedeutung dieses Konzepts in der Mathematik und im Alltag zu erkennen.