Was Sind Gebrochen Rationale Funktionen

Haben Sie sich jemals gefragt, wie Ingenieure Brücken bauen, wie Ökonomen Markttrends vorhersagen oder wie Physiker Flugbahnen berechnen? Oftmals stecken dahinter mathematische Modelle, die auf einer speziellen Art von Funktionen basieren: den gebrochen rationalen Funktionen. Keine Sorge, der Name klingt komplizierter als die eigentliche Idee! Viele scheuen sich vor dem Thema Mathematik, aber wir wollen Ihnen zeigen, dass es gar nicht so beängstigend sein muss. Gemeinsam werden wir die Welt der gebrochen rationalen Funktionen erkunden, ihre Geheimnisse lüften und Ihnen zeigen, wie sie in der realen Welt Anwendung finden.

Was genau sind gebrochen rationale Funktionen?

Im Kern ist eine gebrochen rationale Funktion einfach ein Bruch, bei dem sowohl der Zähler als auch der Nenner Polynome sind. Ein Polynom ist ein mathematischer Ausdruck, der aus Variablen (meistens 'x') und Koeffizienten besteht, die nur durch Addition, Subtraktion und Multiplikation verbunden sind und bei denen die Variablen nicht-negative ganzzahlige Exponenten haben. Ein einfaches Beispiel für ein Polynom wäre 3x² + 2x - 1.

Eine gebrochen rationale Funktion hat also die Form:

f(x) = P(x) / Q(x)

Wobei P(x) und Q(x) jeweils Polynome sind. Wichtig ist, dass Q(x) nicht das Nullpolynom sein darf (also nicht gleich Null sein darf), da eine Division durch Null in der Mathematik nicht definiert ist.

Beispiele für gebrochen rationale Funktionen:

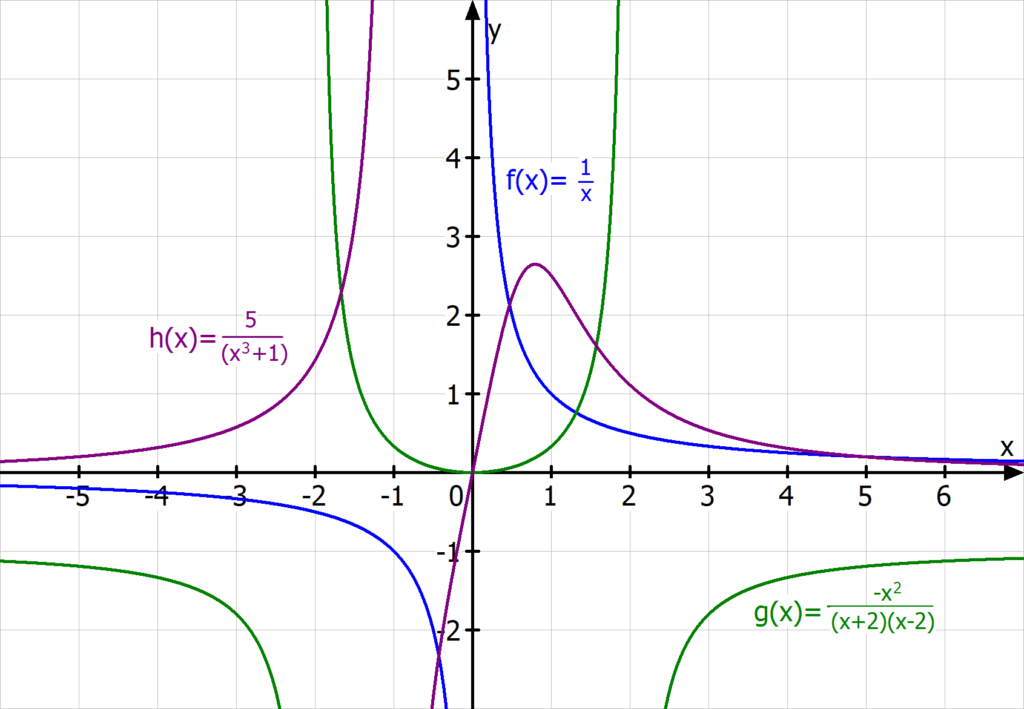
• f(x) = (x + 1) / (x - 2)
• g(x) = (2x² - 3) / (x + 5)
• h(x) = 1 / x (Ja, auch das ist eine gebrochen rationale Funktion!)

Kein Beispiel: f(x) = √(x) / (x+1) (weil √(x) kein Polynom ist)

Warum sind sie so wichtig?

Gebrochen rationale Funktionen sind vielseitig einsetzbar und spielen in vielen Bereichen eine entscheidende Rolle. Hier sind nur einige Beispiele:

• Physik: Die Beschreibung von Kräften, Feldern und Bewegungen erfordert oft gebrochen rationale Funktionen.
• Chemie: Reaktionskinetik und Konzentrationsberechnungen nutzen diese Funktionen.
• Wirtschaft: Angebots- und Nachfragekurven, Kostenfunktionen und Gewinnoptimierungen lassen sich damit modellieren.
• Ingenieurwesen: Signalverarbeitung, Regelungstechnik und die Analyse von Netzwerken greifen auf gebrochen rationale Funktionen zurück.

Denken Sie an das Beispiel einer Brücke. Ingenieure müssen die Belastung der Brücke durch Wind, Gewicht und andere Faktoren berechnen. Gebrochen rationale Funktionen helfen ihnen dabei, diese komplexen Beziehungen zu modellieren und sicherzustellen, dass die Brücke stabil und sicher ist. Laut einer Studie des American Society of Civil Engineers werden komplexe mathematische Modelle, einschließlich solcher, die auf gebrochen rationalen Funktionen basieren, verwendet, um die Sicherheit und Lebensdauer von Brücken zu gewährleisten.

Was macht gebrochen rationale Funktionen besonders?

Im Vergleich zu einfachen linearen oder quadratischen Funktionen besitzen gebrochen rationale Funktionen einige besondere Eigenschaften, die sie so nützlich, aber auch etwas anspruchsvoller machen.

Definitionslücken

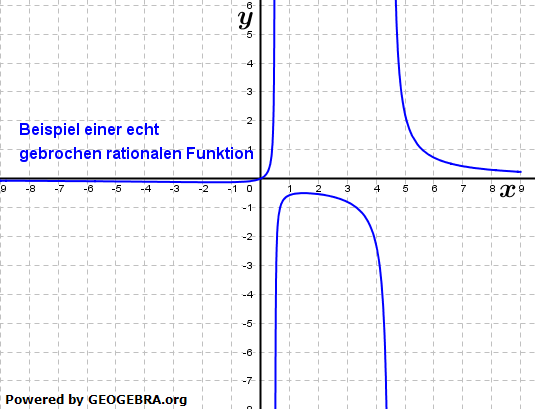
Ein entscheidender Aspekt sind die Definitionslücken. Eine Definitionslücke liegt vor, wenn der Nenner Q(x) gleich Null wird. An diesen Stellen ist die Funktion nicht definiert, da die Division durch Null nicht erlaubt ist. Die Graphen von gebrochen rationalen Funktionen weisen an diesen Stellen oft Asymptoten auf.

Beispiel: Bei der Funktion f(x) = 1 / (x - 2) ist x = 2 eine Definitionslücke, da der Nenner für x = 2 gleich Null wird. Der Graph der Funktion nähert sich einer senkrechten Linie (einer vertikalen Asymptote) bei x = 2.

Asymptoten

Asymptoten sind Linien, denen sich der Graph der Funktion immer weiter annähert, ohne sie jemals zu berühren (oder zu schneiden). Es gibt drei Arten von Asymptoten:

• Vertikale Asymptoten: Sie treten an den Definitionslücken auf, wie bereits erwähnt.
• Horizontale Asymptoten: Sie beschreiben das Verhalten der Funktion, wenn x gegen plus oder minus unendlich geht. Die horizontale Asymptote hängt vom Grad der Polynome P(x) und Q(x) ab.
• Schräge Asymptoten: Sie treten auf, wenn der Grad des Zählerpolynoms P(x) um genau 1 größer ist als der Grad des Nennerpolynoms Q(x).

Das Verständnis von Asymptoten ist entscheidend für das Skizzieren des Graphen einer gebrochen rationalen Funktion.

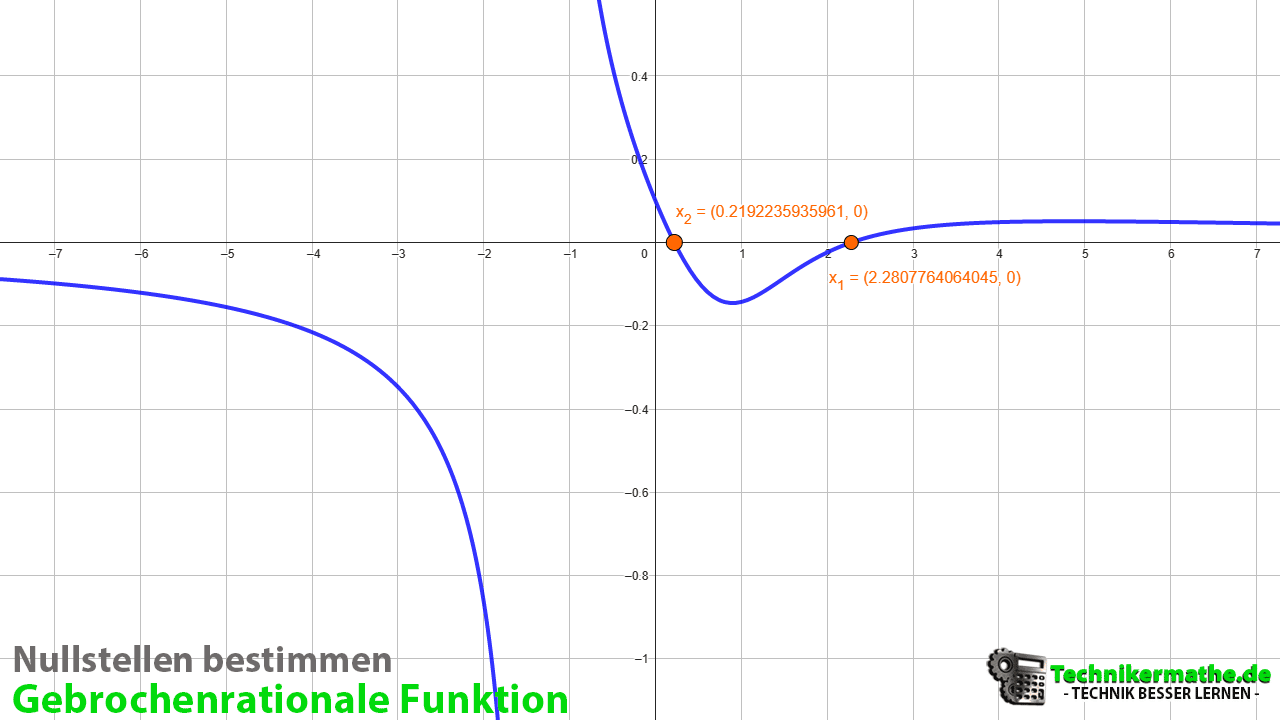
Nullstellen

Die Nullstellen einer gebrochen rationalen Funktion sind die Werte von x, für die die Funktion den Wert Null annimmt. Diese entsprechen den Nullstellen des Zählerpolynoms P(x), solange diese Werte keine Definitionslücken sind.

Beispiel: Bei der Funktion f(x) = (x + 1) / (x - 2) ist x = -1 eine Nullstelle, da der Zähler für x = -1 gleich Null wird.

Wie man mit gebrochen rationalen Funktionen arbeitet

Hier sind einige praktische Tipps für den Umgang mit gebrochen rationalen Funktionen:

1. Definitionslücken finden: Setzen Sie den Nenner Q(x) gleich Null und lösen Sie nach x auf.
2. Nullstellen finden: Setzen Sie den Zähler P(x) gleich Null und lösen Sie nach x auf (überprüfen Sie, ob die Lösungen Definitionslücken sind).
3. Asymptoten bestimmen: Untersuchen Sie das Verhalten der Funktion an den Definitionslücken (vertikale Asymptoten) und für große Werte von x (horizontale oder schräge Asymptoten).
4. Wertetabelle erstellen: Berechnen Sie einige Funktionswerte, um ein besseres Gefühl für den Verlauf des Graphen zu bekommen.
5. Graph skizzieren: Zeichnen Sie die Definitionslücken, Nullstellen und Asymptoten in ein Koordinatensystem ein und verbinden Sie die Punkte der Wertetabelle unter Berücksichtigung der Asymptoten.

Tools zur Hilfe: Es gibt zahlreiche Online-Rechner und Grafikprogramme (wie Geogebra), die Ihnen beim Lösen von Gleichungen, Finden von Nullstellen und Skizzieren von Graphen gebrochen rationaler Funktionen helfen können. Nutzen Sie diese Ressourcen, um Ihr Verständnis zu vertiefen und komplexe Probleme zu lösen.

Fazit

Gebrochen rationale Funktionen mögen auf den ersten Blick einschüchternd wirken, aber mit dem richtigen Verständnis und den richtigen Werkzeugen können Sie ihre Komplexität meistern. Sie sind ein mächtiges Werkzeug, das in vielen Bereichen Anwendung findet und uns hilft, die Welt um uns herum besser zu verstehen. Scheuen Sie sich nicht, sich mit ihnen auseinanderzusetzen, experimentieren Sie und entdecken Sie ihre faszinierenden Eigenschaften. Indem Sie sich die Grundlagen aneignen und üben, werden Sie feststellen, dass gebrochen rationale Funktionen gar nicht so "gebrochen" sind, wie sie scheinen!