Wie Berechne Ich Die Standardabweichung

Standardabweichung verstehen: Dein ultimativer Leitfaden
Hallo! Lass uns zusammen die Standardabweichung meistern. Keine Sorge, es ist einfacher als du denkst. Wir brechen alles in verständliche Schritte auf. Denk dran, Übung macht den Meister!
Was ist die Standardabweichung überhaupt?
Die Standardabweichung ist ein Maß für die Streuung von Daten. Sie zeigt, wie weit die einzelnen Werte von dem Durchschnitt (Mittelwert) entfernt sind. Eine hohe Standardabweichung bedeutet, dass die Daten stark gestreut sind. Eine niedrige Standardabweichung bedeutet, dass die Daten nahe am Durchschnitt liegen.
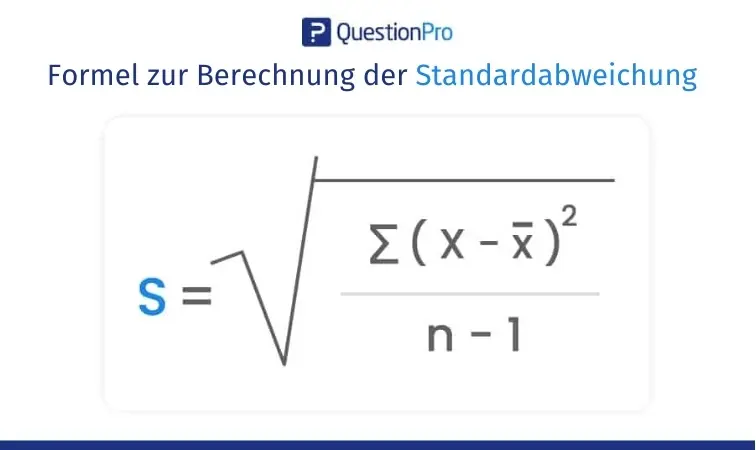
Die Formel: Kein Grund zur Panik!
Die Formel sieht kompliziert aus, aber wir gehen sie Schritt für Schritt durch. Hier ist sie:
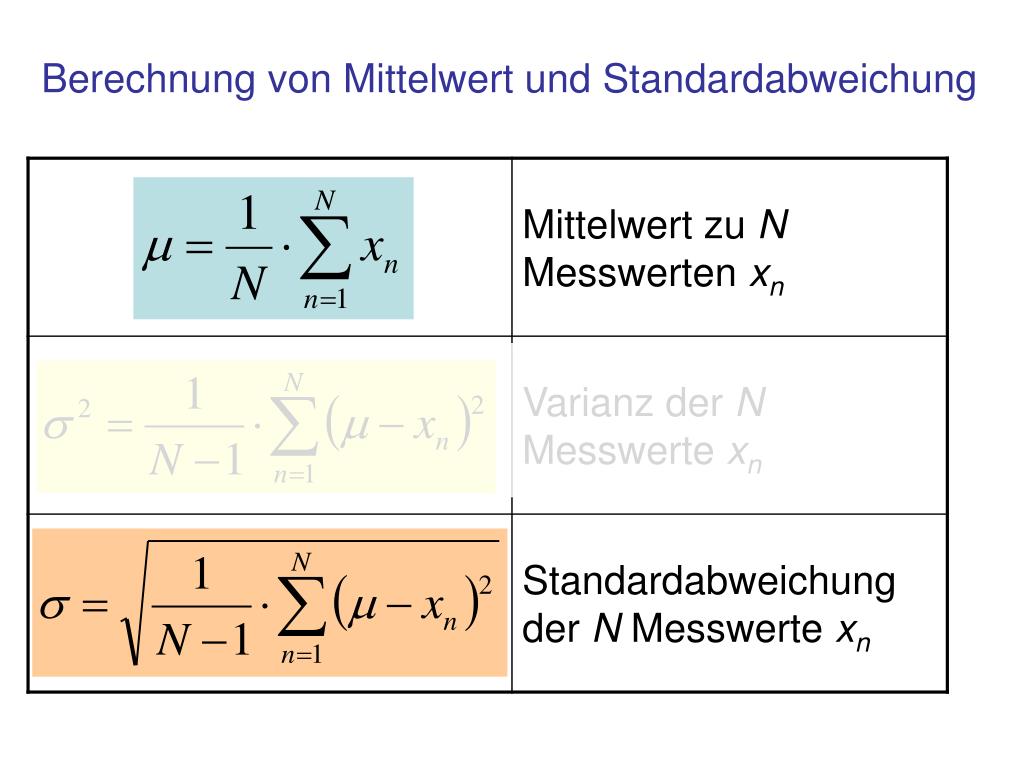
σ = √[ Σ (xi - μ)² / N ]
σ (Sigma) steht für die Standardabweichung. xi sind die einzelnen Werte in deinem Datensatz. μ (Mü) ist der Mittelwert deines Datensatzes. N ist die Anzahl der Werte in deinem Datensatz. Σ (Sigma groß) ist das Summenzeichen, das heißt, du musst alle Ergebnisse der nachfolgenden Rechnung addieren.
Schritt-für-Schritt-Anleitung zur Berechnung
Hier ist eine einfache Anleitung, wie du die Standardabweichung berechnest. Wir verwenden ein kleines Beispiel, um es zu verdeutlichen. Stell dir vor, du hast die folgenden Zahlen: 2, 4, 6, 8, 10.
Schritt 1: Berechne den Mittelwert (Durchschnitt)
Addiere alle Zahlen und teile sie durch die Anzahl der Zahlen. In unserem Beispiel: (2 + 4 + 6 + 8 + 10) / 5 = 6. Der Mittelwert (μ) ist also 6. Wir brauchen ihn später!
Schritt 2: Berechne die Abweichung vom Mittelwert für jeden Wert
Subtrahiere den Mittelwert von jedem einzelnen Wert (xi). Für unsere Zahlen: * 2 - 6 = -4 * 4 - 6 = -2 * 6 - 6 = 0 * 8 - 6 = 2 * 10 - 6 = 4
Schritt 3: Quadriere die Abweichungen
Nimm jede Abweichung, die du gerade berechnet hast, und quadriere sie. Das bedeutet, multipliziere jede Zahl mit sich selbst. Für unser Beispiel: * (-4)² = 16 * (-2)² = 4 * (0)² = 0 * (2)² = 4 * (4)² = 16
Schritt 4: Berechne die Summe der quadrierten Abweichungen
Addiere alle quadrierten Abweichungen. In unserem Beispiel: 16 + 4 + 0 + 4 + 16 = 40. Dies ist die Summe der quadrierten Abweichungen.
Schritt 5: Teile durch die Anzahl der Werte (N)
Teile die Summe der quadrierten Abweichungen durch die Anzahl der Werte in deinem Datensatz. In unserem Beispiel: 40 / 5 = 8. Das ist die Varianz.
Schritt 6: Ziehe die Quadratwurzel
Nimm die Quadratwurzel des Ergebnisses aus Schritt 5. In unserem Beispiel: √8 ≈ 2.83. Das ist die Standardabweichung!
Wichtige Hinweise
Manchmal musst du die Stichprobenstandardabweichung berechnen. Das machst du, wenn du nur eine Stichprobe aus einer größeren Population hast. Die Formel ist leicht anders. Anstatt durch N zu teilen, teilst du durch N-1. Das macht die Standardabweichung etwas größer. Das gleicht aus, dass du nur eine Stichprobe hast.
Achte auf die Einheiten. Wenn deine Daten in Metern sind, ist die Standardabweichung auch in Metern. Überprüfe deine Berechnungen sorgfältig. Ein kleiner Fehler kann zu einem großen Unterschied im Ergebnis führen.
Zusammenfassung
Die Standardabweichung misst die Streuung deiner Daten. Berechne den Mittelwert, die Abweichungen, quadrierten Abweichungen und deren Summe. Teile durch N (oder N-1 für Stichproben) und ziehe die Quadratwurzel. Vergiss die Einheiten nicht! Du hast das drauf!