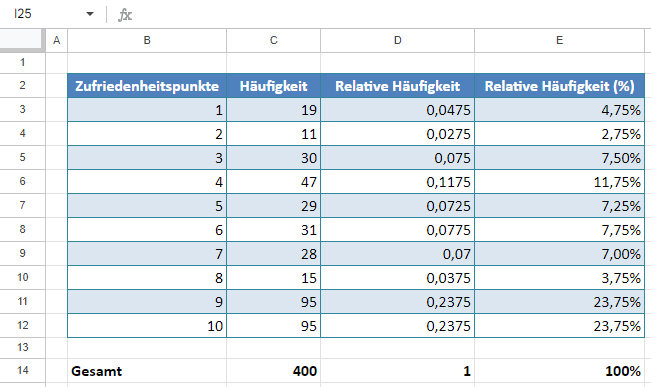
Wie Berechnet Man Relative Häufigkeiten

Was sind relative Häufigkeiten?

Stell dir vor, du hast eine Tüte mit gemischten Bonbons. Es gibt rote, gelbe und grüne Bonbons. Du möchtest wissen, welcher Anteil der Bonbons rot ist. Das ist, wo die relative Häufigkeit ins Spiel kommt.

Die relative Häufigkeit hilft uns zu verstehen, wie oft ein bestimmtes Ereignis im Vergleich zur Gesamtzahl aller Ereignisse vorkommt. Es ist wie eine Prozentzahl, die uns sagt, wie verbreitet etwas ist. Denk daran, es ist ein Verhältnis von *Teil* zu *Ganzem*.

Wie berechnet man sie?

Die Formel ist super einfach. Zuerst zählst du, wie oft das Ereignis, das dich interessiert, eintritt. Nennen wir diese Zahl die absolute Häufigkeit. Dann zählst du, wie viele Ereignisse es insgesamt gab.

Um die relative Häufigkeit zu berechnen, teilst du die absolute Häufigkeit durch die Gesamtzahl der Ereignisse. Das Ergebnis ist eine Dezimalzahl. Diese Dezimalzahl kannst du dann mit 100 multiplizieren, um sie als Prozentzahl auszudrücken. Stell es dir wie einen Kuchen vor. Die relative Häufigkeit ist ein Kuchenstück im Verhältnis zum ganzen Kuchen!

Formel: Relative Häufigkeit = (Absolute Häufigkeit / Gesamtzahl der Ereignisse) * 100%

Ein Beispiel mit Bonbons

Nehmen wir an, du hast 20 Bonbons in deiner Tüte. Davon sind 8 rot, 7 gelb und 5 grün. Du möchtest die relative Häufigkeit der roten Bonbons berechnen. Die absolute Häufigkeit der roten Bonbons ist 8.

Die Gesamtzahl der Bonbons ist 20. Also, die relative Häufigkeit der roten Bonbons ist 8/20. Das ergibt 0,4. Wenn wir das mit 100 multiplizieren, erhalten wir 40%. Das bedeutet, dass 40% deiner Bonbons rot sind. Stell dir vor: von 100 Bonbons wären 40 rot!

Für die gelben Bonbons wäre die Rechnung 7/20 = 0,35, also 35%. Und für die grünen Bonbons 5/20 = 0,25, also 25%. Zusammen ergeben die Prozentzahlen 100%, was bedeutet, dass wir alle Bonbons berücksichtigt haben.

Noch ein Beispiel: Eine Umfrage

Stell dir vor, du führst eine Umfrage unter 50 Leuten durch. Du fragst, welche Eissorte sie am liebsten mögen: Vanille, Schokolade oder Erdbeere. 25 Leute sagen Vanille, 15 Leute sagen Schokolade und 10 Leute sagen Erdbeere.

Die Gesamtzahl der Befragten ist 50. Die absolute Häufigkeit der Vanille-Liebhaber ist 25. Die relative Häufigkeit der Vanille-Liebhaber ist also 25/50 = 0,5. Das entspricht 50%. Die Hälfte aller Befragten liebt Vanille am meisten.

Für Schokolade: 15/50 = 0,3, also 30%. Und für Erdbeere: 10/50 = 0,2, also 20%. Auch hier ergeben alle Prozentzahlen zusammen 100%.

Warum sind relative Häufigkeiten nützlich?

Relative Häufigkeiten sind super nützlich, um Daten zu vergleichen. Stell dir vor, du hast zwei Klassen: Klasse A mit 20 Schülern und Klasse B mit 30 Schülern. In Klasse A haben 10 Schüler eine 1 in Mathe geschrieben. In Klasse B haben 12 Schüler eine 1 in Mathe geschrieben.

Wenn man nur die absoluten Häufigkeiten vergleicht (10 in Klasse A und 12 in Klasse B), könnte man denken, dass Klasse B besser in Mathe ist. Aber wenn wir die relativen Häufigkeiten berechnen, sehen wir ein anderes Bild.

In Klasse A ist die relative Häufigkeit der 1er-Schüler 10/20 = 0,5, also 50%. In Klasse B ist die relative Häufigkeit 12/30 = 0,4, also 40%. Obwohl in Klasse B mehr Schüler eine 1 geschrieben haben, ist der *Anteil* der 1er-Schüler in Klasse A höher. Relative Häufigkeiten ermöglichen also einen fairen Vergleich zwischen verschiedenen Datensätzen.

Zusammenfassung

Relative Häufigkeiten sind ein mächtiges Werkzeug, um Daten zu analysieren und zu vergleichen. Sie helfen uns zu verstehen, wie oft etwas im Verhältnis zu einem Ganzen vorkommt. Denk an Bonbons, Umfragen und Schulnoten. Mit der einfachen Formel (Absolute Häufigkeit / Gesamtzahl der Ereignisse) * 100% kannst du die relative Häufigkeit für fast alles berechnen! Visualisiere die Daten als Teile eines Kuchens, und du wirst das Konzept leicht verstehen.