Wie Rechnet Man Dezimalzahlen In Brüche

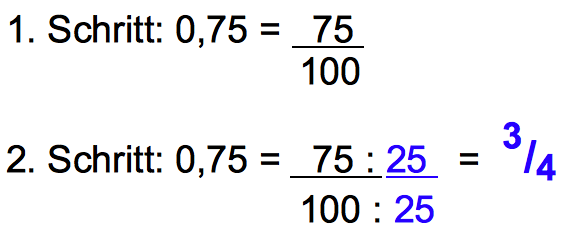
Dezimalzahlen sind allgegenwärtig in unserem Alltag, von Preisen im Supermarkt bis hin zu Messwerten in wissenschaftlichen Experimenten. Manchmal ist es jedoch notwendig oder nützlich, eine Dezimalzahl in einen Bruch umzuwandeln. Dies kann die Weiterverarbeitung erleichtern, insbesondere wenn es um exakte Berechnungen geht, oder es kann schlichtweg das Verständnis für den Wert der Zahl verbessern. In diesem Artikel werden wir Schritt für Schritt erklären, wie man Dezimalzahlen in Brüche umwandelt, und dabei sowohl einfache als auch komplexere Fälle berücksichtigen.

Grundlagen der Umwandlung

Der Schlüssel zur Umwandlung einer Dezimalzahl in einen Bruch liegt im Verständnis der Stellenwerte nach dem Dezimalkomma. Jede Stelle repräsentiert eine Potenz von 10: die erste Stelle ist die Zehntelstelle (1/10), die zweite die Hundertstelstelle (1/100), die dritte die Tausendstelstelle (1/1000) und so weiter.

Endliche Dezimalzahlen

Endliche Dezimalzahlen sind solche, die nach einer bestimmten Anzahl von Stellen enden. Die Umwandlung dieser Zahlen ist relativ einfach:

1. Schritt 1: Schreibe die Dezimalzahl ohne das Dezimalkomma als Zähler des Bruchs.
2. Schritt 2: Bestimme die Anzahl der Stellen nach dem Dezimalkomma. Diese Anzahl entspricht der Anzahl der Nullen im Nenner, der immer eine Potenz von 10 ist.
3. Schritt 3: Vereinfache den Bruch, indem du Zähler und Nenner durch ihren größten gemeinsamen Teiler (ggT) dividierst.

Beispiel: Wandeln wir die Dezimalzahl 0,75 in einen Bruch um.

1. Zähler: 75
2. Anzahl der Stellen nach dem Komma: 2. Also ist der Nenner 100.
3. Bruch: 75/100. Der ggT von 75 und 100 ist 25. Dividieren wir Zähler und Nenner durch 25, erhalten wir 3/4.

Daher ist 0,75 äquivalent zu 3/4.

Ein weiteres Beispiel: 1,25

1. Zähler: 125
2. Anzahl der Stellen nach dem Komma: 2. Also ist der Nenner 100.
3. Bruch: 125/100. Der ggT von 125 und 100 ist 25. Dividieren wir Zähler und Nenner durch 25, erhalten wir 5/4.

Daher ist 1,25 äquivalent zu 5/4. Dies kann auch als gemischte Zahl geschrieben werden: 1 1/4.

Periodische Dezimalzahlen

Periodische Dezimalzahlen sind solche, bei denen sich eine Ziffer oder eine Gruppe von Ziffern unendlich wiederholt. Die Umwandlung dieser Zahlen ist etwas komplexer.

Es gibt zwei Arten von periodischen Dezimalzahlen: rein periodische und gemischt periodische.

• Rein periodische Dezimalzahlen: Die Periode beginnt direkt nach dem Dezimalkomma (z.B. 0,3333...).
• Gemischt periodische Dezimalzahlen: Es gibt nicht-periodische Ziffern zwischen dem Dezimalkomma und der Periode (z.B. 0,16666...).

Rein periodische Dezimalzahlen umwandeln

1. Schritt 1: Sei x die periodische Dezimalzahl.
2. Schritt 2: Multipliziere x mit 10ⁿ, wobei n die Anzahl der Ziffern in der Periode ist.
3. Schritt 3: Subtrahiere x von 10ⁿx. Dies eliminiert den periodischen Teil.
4. Schritt 4: Löse die Gleichung nach x auf.

Beispiel: Wandeln wir 0,3333... in einen Bruch um.

1. x = 0,3333...
2. Die Periode ist '3', also n = 1. Multipliziere x mit 10¹ = 10: 10x = 3,3333...
3. Subtrahiere x von 10x: 10x - x = 3,3333... - 0,3333... => 9x = 3
4. Löse nach x auf: x = 3/9 = 1/3

Daher ist 0,3333... äquivalent zu 1/3.

Gemischt periodische Dezimalzahlen umwandeln

1. Schritt 1: Sei x die gemischt periodische Dezimalzahl.
2. Schritt 2: Multipliziere x mit 10^m, wobei m die Anzahl der nicht-periodischen Ziffern nach dem Dezimalkomma ist. Nennen wir das Ergebnis y.
3. Schritt 3: Multipliziere x mit 10^(m+n), wobei n die Anzahl der Ziffern in der Periode ist. Nennen wir das Ergebnis z.
4. Schritt 4: Subtrahiere y von z. Dies eliminiert den periodischen Teil.
5. Schritt 5: Löse die Gleichung nach x auf.

Beispiel: Wandeln wir 0,16666... in einen Bruch um.

1. x = 0,16666...
2. m = 1 (die '1' ist die nicht-periodische Ziffer). y = 10¹x = 1,6666...
3. n = 1 (die '6' ist die Periode). z = 10⁽¹⁺¹⁾x = 10²x = 100x = 16,6666...
4. Subtrahiere y von z: 100x - 10x = 16,6666... - 1,6666... => 90x = 15
5. Löse nach x auf: x = 15/90 = 1/6

Daher ist 0,16666... äquivalent zu 1/6.

Reale Anwendungen

Die Umwandlung von Dezimalzahlen in Brüche ist in vielen Bereichen nützlich:

• Kochen: Viele Rezepte verwenden Bruchzahlen (z.B. 1/2 Tasse Mehl). Wenn ein Rezept Dezimalangaben macht (z.B. 0,5 Tassen), kann die Umwandlung in einen Bruch das Abmessen erleichtern.
• Finanzen: Bei der Berechnung von Zinsen oder Rabatten kann die Umwandlung von Dezimalzahlen in Brüche zu genaueren Ergebnissen führen. Zum Beispiel ist ein Rabatt von 0,25 des ursprünglichen Preises einfacher als 1/4 des ursprünglichen Preises zu verstehen und zu berechnen.
• Mathematik und Physik: In wissenschaftlichen Berechnungen kann es vorteilhaft sein, Werte als Brüche darzustellen, um exakte Lösungen zu erhalten und Rundungsfehler zu vermeiden.
• Programmierung: Bestimmte Programmiersprachen oder Anwendungen behandeln Brüche anders als Dezimalzahlen. Die Umwandlung kann notwendig sein, um Kompatibilität zu gewährleisten oder Algorithmen zu optimieren.

Beispiel aus der Finanzwelt: Angenommen, Sie möchten den effektiven Jahreszins einer Anlage berechnen, die einen nominalen Jahreszins von 5,25% hat, der vierteljährlich verzinst wird. Die Dezimalzahl 0,0525 muss in einen Bruch umgewandelt werden, um die Zinseszinsformel korrekt anzuwenden und genaue Ergebnisse zu erhalten.

Hilfreiche Tools und Ressourcen

Es gibt zahlreiche Online-Rechner und Apps, die die Umwandlung von Dezimalzahlen in Brüche erleichtern. Diese Tools können besonders nützlich sein, wenn es um komplexere periodische Dezimalzahlen geht. Es ist jedoch wichtig, das zugrundeliegende Prinzip zu verstehen, um die Ergebnisse zu interpretieren und sicherzustellen, dass sie sinnvoll sind.

Wichtige Anmerkung: Nicht alle Dezimalzahlen lassen sich exakt als Brüche darstellen. Irrationale Zahlen wie π (Pi) haben eine unendliche, nicht-periodische Dezimaldarstellung und können daher nur approximativ durch Brüche dargestellt werden.

Zusammenfassung

Die Umwandlung von Dezimalzahlen in Brüche ist eine grundlegende Fähigkeit mit praktischen Anwendungen in vielen Bereichen. Indem Sie die Stellenwerte nach dem Dezimalkomma verstehen und die entsprechenden Umwandlungsmethoden anwenden, können Sie Dezimalzahlen problemlos in Brüche umwandeln. Übung macht den Meister! Je mehr Sie üben, desto vertrauter werden Sie mit dem Prozess und desto einfacher wird es, Dezimalzahlen in Brüche umzuwandeln. Vergessen Sie nicht, das Ergebnis immer zu vereinfachen, um den Bruch in seiner einfachsten Form darzustellen. Nutzen Sie die hier vorgestellten Methoden und Beispiele als Grundlage, um Ihre Kenntnisse zu vertiefen und Ihre Fähigkeiten in diesem Bereich zu verbessern.

Experimentieren Sie mit verschiedenen Dezimalzahlen und versuchen Sie, sie in Brüche umzuwandeln. Fordern Sie sich selbst heraus, indem Sie komplexere periodische Dezimalzahlen betrachten. Mit der Zeit werden Sie ein Experte in der Umwandlung von Dezimalzahlen in Brüche!