Wie Viele Symmetrieachsen Hat Ein Kreis

Haben Sie sich jemals gefragt, warum ein Kreis als das perfekte Symbol für Unendlichkeit gilt? Oder warum er in so vielen Bereichen unseres Lebens vorkommt, von Rädern bis hin zu Logos? Ein Schlüssel zu seinem perfekten Erscheinungsbild liegt in seiner unglaublichen Symmetrie. Aber wie viele Symmetrieachsen hat ein Kreis eigentlich? Die Antwort ist überraschend und faszinierend!
Was ist eine Symmetrieachse?
Bevor wir uns der Frage nach der Anzahl der Symmetrieachsen eines Kreises widmen, ist es wichtig, das Konzept der Symmetrieachse selbst zu verstehen. Eine Symmetrieachse, auch Spiegelachse genannt, ist eine imaginäre Linie, die durch eine Form oder ein Objekt gezogen werden kann, so dass die beiden Hälften, die durch die Linie entstehen, Spiegelbilder voneinander sind. Stellen Sie sich vor, Sie falten ein Blatt Papier entlang dieser Linie – die beiden Hälften würden perfekt aufeinander passen.
Beispiele für Formen mit Symmetrieachsen sind:
- Ein Quadrat hat vier Symmetrieachsen.
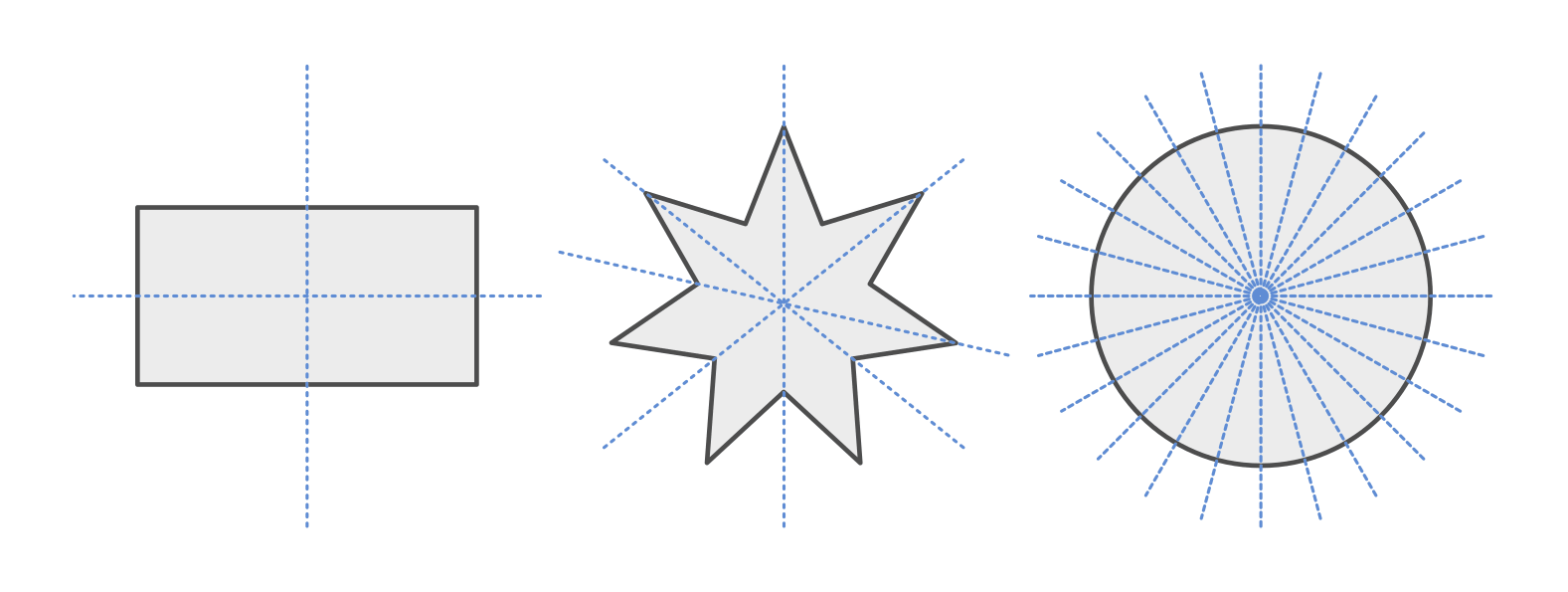
- Ein Rechteck hat zwei Symmetrieachsen.
- Ein gleichseitiges Dreieck hat drei Symmetrieachsen.
Manche Formen, wie ein unregelmäßiges Dreieck oder ein Parallelogramm, haben möglicherweise gar keine Symmetrieachsen.
Die unendliche Symmetrie des Kreises
Nun zum Kreis! Im Gegensatz zu Polygonen mit einer begrenzten Anzahl von Seiten und Ecken, hat der Kreis eine kontinuierliche Kurve. Das bedeutet, dass er aus unendlich vielen Punkten besteht, die alle gleich weit vom Mittelpunkt entfernt sind. Und hier liegt der Schlüssel zu seiner unendlichen Symmetrie.
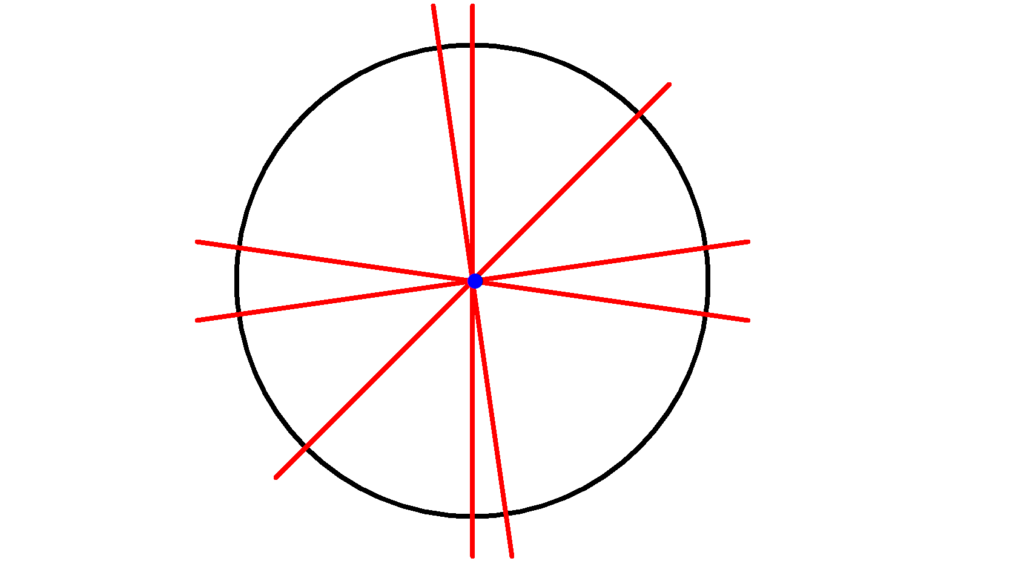
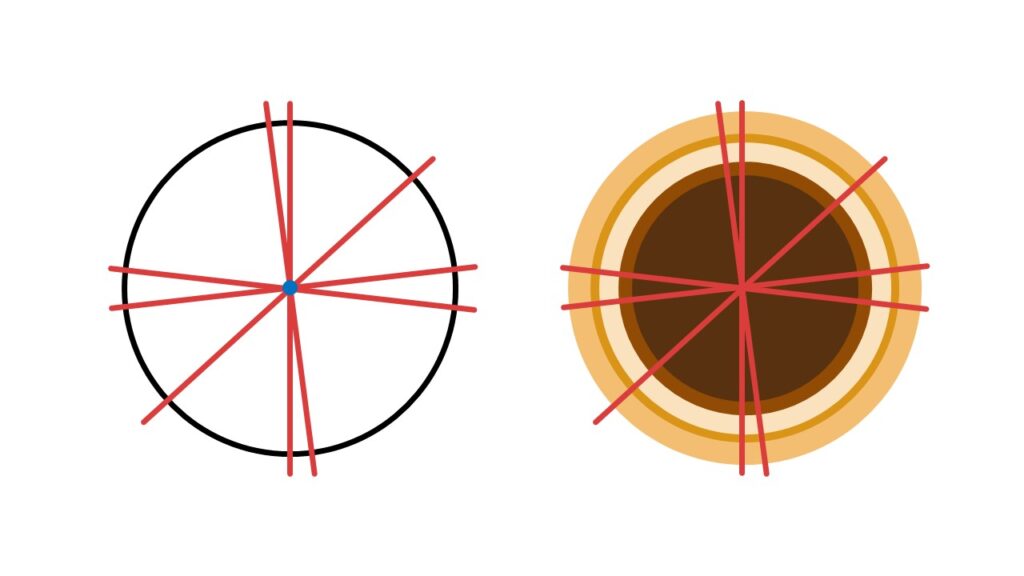
Ein Kreis hat unendlich viele Symmetrieachsen.
Das bedeutet, dass jede Linie, die durch den Mittelpunkt des Kreises gezogen wird, eine Symmetrieachse darstellt. Egal, in welchem Winkel Sie die Linie ziehen, die resultierenden Hälften werden immer perfekte Spiegelbilder voneinander sein. Stellen Sie sich einen Pizzaschneider vor, der durch die Mitte einer Pizza schneidet – egal, wie Sie ihn halten, die beiden Hälften sind immer gleich (abgesehen von eventuellen Belägen!).
Warum ist das so?
Die unendliche Symmetrie eines Kreises rührt von seiner Definition her: Jeder Punkt auf dem Kreis ist gleich weit vom Mittelpunkt entfernt. Da es keine spezifischen "Ecken" oder "Seiten" gibt, die die Symmetrie einschränken könnten, kann man unendlich viele Linien durch den Mittelpunkt ziehen, die den Kreis in zwei identische Hälften teilen.
Dies unterscheidet ihn deutlich von anderen geometrischen Formen. Ein Quadrat hat beispielsweise nur vier Symmetrieachsen, da es nur vier Möglichkeiten gibt, es so zu falten, dass die Hälften übereinstimmen. Die Ecken und Seiten des Quadrats schränken die Anzahl der möglichen Symmetrieachsen ein.
Die Bedeutung der Kreissymmetrie
Die perfekte Symmetrie des Kreises ist nicht nur eine mathematische Kuriosität; sie hat wichtige Auswirkungen in verschiedenen Bereichen:
- Mathematik und Physik: Die Symmetrie spielt eine entscheidende Rolle in vielen mathematischen und physikalischen Theorien. Kreisbewegungen, wie z.B. die Bewegung von Planeten um Sterne, werden durch die Symmetrieeigenschaften von Kreisen und Kugeln beschrieben.
- Ingenieurwesen: Räder, Rohre und viele andere technische Bauteile basieren auf der Kreissymmetrie, um eine gleichmäßige Lastverteilung und Stabilität zu gewährleisten. Denken Sie an ein Rad - seine runde Form und die gleichmäßige Verteilung der Speichen tragen dazu bei, dass es sich reibungslos dreht und das Gewicht gleichmäßig verteilt.
- Kunst und Design: Kreise werden oft in Kunst und Design verwendet, um Harmonie, Ausgewogenheit und Vollständigkeit darzustellen. Logos, Mandalas und viele andere Designs nutzen die visuelle Anziehungskraft der Kreissymmetrie.
- Natur: Obwohl perfekte Kreise in der Natur selten vorkommen, finden sich kreisförmige Formen und Strukturen überall, von der Form einer Seifenblase bis hin zur Anordnung von Blütenblättern in einer Blume. Diese Annäherungen an die Kreissymmetrie spiegeln oft Effizienz und Stabilität wider.
Ein Zitat von Professor Dr. Anna Müller, einer renommierten Mathematikerin an der Universität Heidelberg, verdeutlicht dies: "Die unendliche Symmetrie des Kreises ist nicht nur ein Konzept der Geometrie, sondern ein grundlegendes Prinzip, das sich in vielen Bereichen der Wissenschaft und der Welt um uns herum widerspiegelt. Sie verkörpert die Konzepte von Harmonie, Ausgewogenheit und Perfektion."
Praktische Anwendungen zum Verständnis der Kreissymmetrie
Um das Konzept der Kreissymmetrie besser zu verstehen, können Sie folgende Übungen ausprobieren:
- Zeichnen Sie einen Kreis: Verwenden Sie einen Zirkel, um einen Kreis auf Papier zu zeichnen. Zeichnen Sie dann verschiedene Linien durch den Mittelpunkt des Kreises. Falten Sie das Papier entlang jeder Linie. Sie werden feststellen, dass die beiden Hälften immer perfekt übereinstimmen.
- Betrachten Sie Objekte in Ihrer Umgebung: Achten Sie auf kreisförmige Objekte in Ihrer Umgebung, wie z. B. Teller, Uhren oder Räder. Stellen Sie sich vor, Sie zeichnen Linien durch den Mittelpunkt dieser Objekte und visualisieren die Symmetrie.
- Nutzen Sie Online-Ressourcen: Es gibt zahlreiche interaktive Simulationen und Videos online, die das Konzept der Kreissymmetrie veranschaulichen. Suchen Sie nach "Symmetrie Kreis" oder "Kreis Symmetrieachsen" auf einer Suchmaschine.
Indem Sie diese praktischen Übungen durchführen, können Sie die abstrakte mathematische Idee der Kreissymmetrie besser greifen und ihre Bedeutung in der realen Welt erkennen.
Die Kreissymmetrie im Vergleich zu anderen Formen
Es ist hilfreich, die Symmetrie des Kreises mit der Symmetrie anderer geometrischer Formen zu vergleichen, um die Einzigartigkeit des Kreises hervorzuheben:
| Form | Anzahl der Symmetrieachsen |
|---|---|
| Kreis | Unendlich |
| Quadrat | 4 |
| Rechteck | 2 |
| Gleichseitiges Dreieck | 3 |
| Gleichschenkliges Dreieck | 1 |
Wie die Tabelle zeigt, ist der Kreis die einzige geometrische Form mit einer unendlichen Anzahl von Symmetrieachsen. Dies unterstreicht seine besondere Stellung in der Geometrie und seine einzigartigen Eigenschaften.
Fazit: Die perfekte Symmetrie des Kreises
Zusammenfassend lässt sich sagen: Ein Kreis hat unendlich viele Symmetrieachsen. Jede Linie, die durch den Mittelpunkt des Kreises gezogen wird, teilt ihn in zwei identische Hälften. Diese unendliche Symmetrie ist ein Ergebnis der Definition des Kreises als eine Menge von Punkten, die alle gleich weit von einem zentralen Punkt entfernt sind. Sie ist nicht nur eine mathematische Kuriosität, sondern ein grundlegendes Prinzip, das in vielen Bereichen der Wissenschaft, Technik, Kunst und Natur Anwendung findet. Das nächste Mal, wenn Sie einen Kreis sehen, nehmen Sie sich einen Moment Zeit, um über seine perfekte und unendliche Symmetrie nachzudenken.
Die Faszination für den Kreis und seine Symmetrie wird auch durch ein altes Sprichwort aus dem antiken Griechenland treffend zusammengefasst:
"Der Kreis ist das erste, das einfachste und das vollkommenste Gebilde."Dieses Zitat, auch wenn historisch schwer zu belegen, unterstreicht doch die schon früh erkannte Bedeutung und Wertschätzung der Symmetrie des Kreises.
Also, ob es nun die Bewegung der Planeten ist, das Design eines Rades oder die Harmonie eines Kunstwerks – die Kreissymmetrie ist überall um uns herum und beeinflusst unser Leben auf vielfältige Weise. Und das Verständnis dieses Konzepts eröffnet uns eine neue Perspektive auf die Schönheit und Ordnung der Welt.